pomóżcie
agatka: Kawałek czworokątnego materiału o obwodzie 3 m przecięto wzdłuż jednego z jego przekątnych.
Powstały dwie chusty o kształcie trójkąta równoramiennego: pierwsza o obwodzie 1,8 m , a
druga o obwodzie 2,8 m .Linia rozcięcia stanowi podstawę pierwszego trójkąta, a dla drugiego
jest ramieniem. Wyznacz wymiary obu chust
6 wrz 10:31
tim: Ja.
6 wrz 10:36
tim: Ja.
6 wrz 10:36
tim:
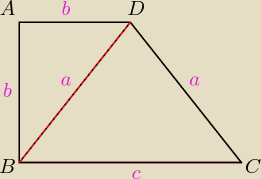
O
ABCD = 3m
O
ABD = 1,8m (|BD| = a jest podstawą, natomiast |AD| = |AB| = b)
O
BCD = 2,8m (|BC| = c jest podstawą, natomiast |BD| = |DC| = a)
a + 2b = 1,8m
2a + c = 2,8m
a + 2b + c = 3m
Wystarczy rozwiązać.
6 wrz 10:42
agatka: pomóżcie mi . Nie umiem zrobić tego zadania a muszę mieć je na jutro
6 wrz 10:43
tim: Już.. Wystarczy moment poczekać... Każdemu pomoc zostanie udzielona
.
6 wrz 10:45
agatka: Dziękuję
6 wrz 10:45
tim: Jak rozwiążesz podaj wynik.
6 wrz 10:47
ktoś: A mógłby do końca to zadanie rozwiązać
6 wrz 10:52
tim: ktośiu, agatko, nie wiem jakie jeszcze inne nicki masz, ale to już powinnieneś/powinnaś sam/a
zrobić:
a + 2b = 1,8m
a + 2b + c = 3m <−−− podstaw tu pierwsze równanie, wyliczysz c.
2a + c = 2,8m
Po obliczeniu 'c' podstaw je do ostatniego równania i obliczysz 'a', natomiast po obliczeniu
'a' obliczysz bez problemu 'b'.
6 wrz 10:55
ktoś: No sory ale nadal nie kumam
6 wrz 10:59
ktoś: Nie wiem jak to zrobić
6 wrz 11:00
tim: ktoś, czego nie rozumiesz, jak rozwiązać?
6 wrz 11:01
ktoś: no
6 wrz 11:01
tim: A w której klasie jestes?
6 wrz 11:01
ktoś: III gim
6 wrz 11:02
tim: Bo układ równań, to się uczymy w gimnazjum rozwiązywać. Ale skoro chcesz, prosze:
a + 2b = 1,8m
a + 2b + c = 3m
2a + c = 2,8m
a + 2b = 1,8m
1,8m + c = 3m
c = 1,2m
2a +
c = 2,8m
a + 2b = 1,8m
c = 1,2m
2a + 1,2m = 2,8m 2a = 1,6m
a = 0,8m
0,8m + 2b = 1,8m 2b = 1m b = 0,5m
c = 1,2m
a = 0,8m
a = 0,8m
b = 0,5m
c = 1,2m
Odczytaj na rysunku i podaj wymiary chust.
6 wrz 11:04
wojtek: jesteś tim jeszcze
6 wrz 16:32
tim: Tak.
6 wrz 16:42
Andrzej: 
16 lis 12:05
moneta:
16 lis 15:55