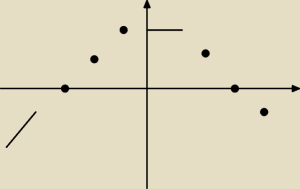
monotoniczność funkcji w punktach odosobnionych? rmcs.pl: Może mi ktoś pomóc w zadaniu? Mam funkcję przypuśćmy że taką jak na rysunkufunkcja dla x∊(−∞, −4) ma wzór x+3 dla x=−3; 0 dla x=−2 ;1 dla x=−1 ; 2 dla x∊<0,1> y=2; dla x=2, y=1, dla x=3 y=0; dla x=4, y=−1 Pytania: Czy mozna uznać że funkcja jest rąsnaca w punktach? To znaczy f rosnąca dla x∊(−∞,−4) ∪ {−3} ∪ {−2} ∪ {−1} Czy ta funkcja jest gdziekolwiek malejąca? Osobiście uważam że funkacja nie może być monotoniczna w punkcie tylko w przedziale, ale spotkałem się z taką interpretacją jaką przedstawiłęm powyżej szukam żetelnej informacji i uzasadnienia definicji, twierdzenia które uzasadnia jedną bądź drugą interpretację

Artur_z_miasta_Neptuna: wszystko zależy jak zbudowany jest zbiór X (dziedzina) jeżeli x=R ... nie ... nie można uznać że funkcja jest rosnąca w punkcie Przeczy temu definicja tylko w przedziale ... więc f↗ w (−∞,−4) jeżeli X = {x∊R; x∊(−∞,−4) ∪ {−3} ∪ {−2} ∪ {−1} ∪(0,1) ... itd.) to tak ... jest rosnąca w pokazanym przez Ciebie przedziale Definicja funkcji rosnącej na przedziale (a,b) ⊂ D_f: ∀_x1,x2 x₁<x₂ ⇒ f(x₁)<f(x₂) nigdzie nie jest malejąca

Artur_z_miasta_Neptuna: definicja nic nie mówi, o tym że punkty x₁ i x₂ muszą być w jakimś otoczeniu siebie ... jedynie, że należą do przedziału X, którego badamy monotoniczność. zbiór liczb Naturalnych także jest funkcją rosnącą (tak tak ... ciąg jest funkcją)