matematykaszkolna.pl
logarytm pytanie asha: Czy log23*log34=log24=2....
28 mar 21:38
Eta:
 1 2 
log43=
=
 log43 log23 
 2 
log23*
= 2
 log23 
28 mar 21:45
PuRXUTM:
 1 log3 4 log3 22 2*log3 2 
=
* log3 4=
=
=
=2
 log3 2 log3 2 log3 2 log3 2 
28 mar 21:48
PuRXUTM: emotka Witaj Eto emotka
 1 
asha Eta tam zastosowała wzór szalony logan b=
loga b jakbyś czasem nie wiedziała
 n 
skąd to się wzięło emotka
28 mar 21:49
Eta: Witam emotka jaki "wzór szalony" ? skoro go zapamiętałeś
28 mar 21:51
PuRXUTM: emotka Ale ogólnie szalony emotka Ale w sumie trafne spostrzeżenie, że nawet jak ja zapamiętałem to on nie jest jakiś straszny
28 mar 21:54
Eta:
 m 
logan (bm) =
*logab emotka
 n 
28 mar 21:56
PuRXUTM: masz jeszcze jakiś fajny ? Bo by się przydał, nie koniecznie z log
28 mar 21:57
Eta: dla y=ax2+bx+c W(xw,yw) yw= c−a*xw2 emotka
28 mar 21:59
Eta:
 x 
1+cosx= 2cos2
 2 
 x 
1−cosx = 2sin2
 2 
28 mar 22:00
PuRXUTM: a jakiś dowodzik ? czy po prostu chcesz żebym się czegoś złego nauczył ? a później na maturze 0%
28 mar 22:01
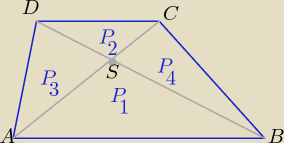Eta: rysunek P(trapezu)= (k+1)2*P2 , k>0 −− skala podobieństwa trójkątów ABS i DCS P3=P4= k*P2 i P1=k2*P2
28 mar 22:04
Eta: cos2α= 2cos2α−1 = 1−2sin2α
 α 
to 1+cos2α= 2cos2α ⇒ 1+cosα=2cos2
 2 
 3α 
1+cos3α= 2cos2
 2 
1−cos4α= 2sin22α itd........ emotka
28 mar 22:08
Eta: Te wzorki przydadzą się na studiach emotka
28 mar 22:09
PuRXUTM: dzięki emotka Ale i tak to zapomnę
28 mar 22:12