wartość bezwzględna bezendu: Dla jakich wartości parametru m równanie ma |x−2|=2m+1 a) jedno rozwiązanie b) dwa rozwiązania a) |x−2|=2m+1 czyli jedno rozwiązanie jak |x−2|=0 2m+1=0 2m=−1

	1
m=−
	2

b) |x+2|=2m+1 |x−2|>0 2m+1>0 2m>−1

	1
m>−
	2

	1
m∊(−		;∞)
	2

Dominik:

jikA: .

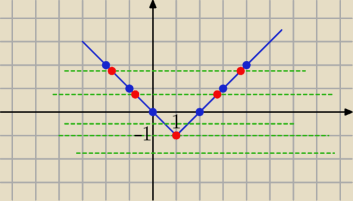
Eta: Dobrze co widać na wykresie f(x)= |x−2|−1 g(x)= 2m

bezendu: dziękuje

bezendu: dla jakich wartości parametru a równanie |x−1|=a²−4a−1 ma dwa dodatnie pierwiastki Δ>0 Δ=4²−4*1*(−1)=20 √Δ=2√5

	4−2√5		2(2−√5)
x1=		=		=2−√5
	2		2

	4+2√5		2(2+√5)
x2=		=		=2+√5
	2		2

i teraz z nierówności wychodzi mi a∊(−∞;2−√5)∪(2√5;∞) ale chyba to jeszcze brakuje jakiegoś warunku albo ja źle rozwiązałem

jikA: Ale Ty nie liczyłeś x₁ oraz x₂.

bezendu: możesz mi podać jakąś wskazówkę jak to zrobić

jikA: Dla jakiej wartości wykres funkcji f(x) = |x − 1| przecina oś OY?

bezendu: czemu oś OY ?

Dominik: narysuj wykres f(x) = |x − 1| i spojrz po ktorej stronie osi rzednych sa dodatnie argumenty.

jikA: Bo po prawej stronie masz argumenty dodatnie a po lewej ujemne.

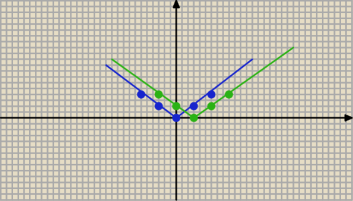
bezendu: zielony to y=|x−1| ( inaczej nie umiałem narysować )

jikA: Masz równanie |x − a| = b teraz aby mieć dwa rozwiązania dodatnie to b musi spełniać warunki b > 0 oraz b < a (ponieważ jeżeli a było by mniejsze od b to miałbyś pierwiastek ujemny. Wynika to z tego x − a = b ∨ x − a = −b x = b + a ∨ x = a − b (a − b > 0 ⇒ a > b).

pigor: ... no bo narysuj sobie wykres funkcji y=|x−1| i zobaczysz, że dla x=0 y= ...? , zatem równanie |x−1|=m i m=a²−4a−1 ma pierwiastki dodatnie ⇔ 0<m< 1 ⇔ ⇔ 0< a²−4a−1< 1 /+5 ⇔ 5< a²−2a*2+4 < 6 ⇔ 5< (a−2)²< 6 ⇔ √ 5< |a−2|< √ 6 ⇔ ⇔ |a−2|>√ 5 i |a−2|< √ 6 ⇔ (a−2<−√ 5 lub a−2>√ 5) i −√ 6< a−2< √ 6 /+2 ⇔ ⇔ ( a< 2−√ 5 lub a >2+√ 5 ) i 2−√ 6< a< 2+√ 6 , teraz narysuj sobie tę koniunkcję uważnie − w miarę dokładnie na − osi liczbowej Oa i odczytaj szukany zbiór wartości a. ...

bezendu: postaram się to narysować na kartce bo tutaj coś mi nie idzie rysowanie

bezendu: narysowałem jeszcze raz http://www7.zippyshare.com/v/25786906/file.html

Mila: Czego nie rozumiesz?

bezendu: jak zrobić to zadanie algebraicznie a nie graficznie

jikA: bezendu przecież Ci napisałem jak zrobić algebraicznie.

Mila: 1)a²−4a−1>0 [Pigor Ci to obliczył] i x−1=a²−4a−1⇔x=a²−4a a stąd warunek : a²−4a>0 i warunek (1) lub x−1=−a²+4a+1⇔x=−a²+4a+2 a stąd warunek: −a²+4a+2 >0 i warunek (1) Jutro sprawdzimy. Dobranoc.

bezendu: @jjka czyli x−1=a²−4a−1 lub x−1=−a²+4a+1

bezendu: Dobranoc

jikA: Nie. Zobacz jakie powinieneś dać warunki.

jikA: Na początku abyś miał dwa rozwiązania jaki warunek musisz dać?

bezendu: 1)a²−4a>0 2) −a²+4a+2>0 takie jak napisała @Mila post 00:02

bezendu: poczekaj można po kolej ? i teraz tak dwa rozwiązania ale czy chodzi o wartość bezwzględną czy to równanie po wartości bezwzględnej ?

jikA: Jaki warunek musisz dać aby mieć dwa rozwiązania dla wartości bezwzględnej.

bezendu: Δ>0

bezendu: a sorry dla wartości bez to |x−1|>0

jikA: Źle piszesz nie |x + 1| > 0 tylko co innego musi być większe od zera.

bezendu: a²−4a−1>0

jikA: Tak teraz rozwiąż ten warunek.

bezendu: no bo |x−1|=0 x=1 |x−1|=4 x−1=4 lub x−1=−4 x=5 x=−3

bezendu: rozwiązać tą nierówność a²−4a−1 a∊(−∞;2−√5)∪(2+√5;∞)

jikA: Okej więc dla tych wartości masz dwa rozwiązania. Teraz jaki musisz dać warunek abyś miał dwa rozwiązania dodatnie zobacz na wpis z 21 : 55.

bezendu: x−a=b lub x−a=−b

jikA: Niech b = a² − 4a − 1 oraz a = 1 i rozważamy równanie postaci |x − a| = b. Warunek abyś miał dwa rozwiązania już dałeś i rozwiązałeś go b > 0 (a² − 4a − 1 > 0) czyli teraz rozwiązując te równanie masz x − a = b ∨ x − a = −b x = a + b ∨ x = a − b Teraz aby dwa rozwiązania był dodatnie to a + b > 0 oraz a − b > 0 warunek a + b > 0 jest spełniony ponieważ a > 0 oraz b > 0 (z warunku na dwa rozwiązania modułu) więc zostało rozwiązać warunek a − b > 0.

bezendu: −a²+4a+2>0 ok zrobię to rana dziękuje za poświęcony czas i wytłumaczenie

bezendu: rano*

bezendu: z pierwszego warunku mam 1) a²−4a−1>0 a∊(−∞;2−√5)∪(2+√5;∞) |x−1|=a²−4a−1 x=a²−4a>0 x=a(a−4)>0 a∊(−∞,0)∪(4;∞0 |x−1|=−a²+4a+1 x=−a²+4a+2 a∊(2−√6;2+√6) i teraz muszę zrobić część wspólna żeby sprawdzić które wartości mieszczą się w tym pierwszym przedziale czyli wyszło mi a∊(2−√6;2−√5)∪(2+√5;2+√6)