okrąg wpisany w trójkąt Tina: W stożek w którym kąt między tworzącą, a podstawą ma miarę 2α wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli. Rozwiązując 'tradycyjnie' wychodzi istny galimatias, po długim czasie wynik ostatecznie wyszedł, ale można się pomylić setki razy poza tym nie mógłbym sobie na takie rozwiązanie pozwolić na maturze... Mam pytanie odnośnie innego sposobu który znalazłem w internecie. 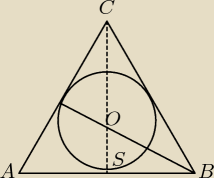"Promień okręgu wpisanego w trójkąt ABC możemy również wyliczyć z trójkąta SBO , gdzie O − środek kuli wpisanej w stożek (zatem BO to dwusieczna kąta B ). Mamy " I teraz pytanie, skąd wiemy, że dwusieczna kąta B dzieli wysokość trójkąta w taki sposób, że odcinek OS to to r tego wpisanego okręgu? Z góry dzięki...

krystek: Dwusieczna zawiera punkty równooddalone od ramion a ta odległośc to właśnie promień. Środek okręgu leży w przecięciu dwusiecznych kątówΔ

Dominik: poniewaz 1) punkt przeciecia srodkowych dzieli je na odcinki o stosunku dlugosci 2:1 2) srodek okregu wpisanego w trojkat zawiera sie w punkcie przeciecia dwusiecznych 3) wysokosc, srodkowa, dwusieczna trojkata rownoramiennego opuszczone na podstawe zawieraja sie w jednej prostej.