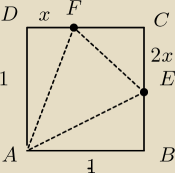
.. rado1234: Bok kwadratu ABCD ma długość równą 1. Na bokach BC i CD wybrano odpowiednio punkty E i F umieszczone tak , by |CE|=2|DF|. Oblicz wartość x = |DF| , dla której pole trójkąta AEF jest najmniejsze. Moze mi ktoś podpowiedzieć jak sie do tego zabrać?

krystek:

rado1234: rysunek zrobilem dobry , niebardzo wiem co dalej

Mila:

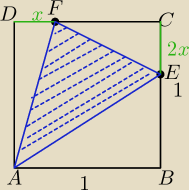
	1
PAEF=12−		(x*1+1*(1−2x)+2x*(1−x))
	2

	1		1
PAEF=x2−		x+
	2		2

	1
xw=		najmniejsza wartość funkcji
	4

	1
dla x=
	4

	1		1		1		1		7
f(		)=		−		+		=
	4		16		8		2		16

rado1234: chyba juz wiem , dzieki