... shm: Dane sa punkty A=(2,1) i B=(5,2). Na prostej o równaniu x−y−1=0 wyznacz taki punkt M, aby pole trójkąta MAB było równe 5. Czy mogę tu skorzystać ze wzoru na pole trójkąta majac jego wierzchołki ?

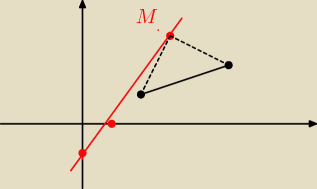
krystek: M=(x, x−1)

pigor: tak możesz oczywiście , a więc ja bym robił np. tak : niech (*) M=( x,y)= (x,x−1)=? i AB^→= [3,1} i AM^→= [x−2,x−1−1]= [x−2,x−2] to P_ΔABM= 5 ⇔ ¹₂ | d(AB^→,AM^→) |= 5 ⇔ ¹₂ | 3(x−2)−1(x−2) |= 5 ⇔ ⇔ | 3x−6−x+2 |= 10 ⇔ |2x−4|= 10 ⇔ 2|x−2|= 10 ⇔ |x−2|= 5 ⇔ ⇔ x−2=−5 lub x−2=5 , a stąd i z (*) (x=−3 i y=−4) lub (x=7 i y=6) ⇒ ⇒ M= (−3,−4) lub M= (7,6) − szukane punkty M ∊ x−y−1=0 . ...

krystek:

	1
lub 5=		IABI*(odległośc M od prostejAB)
	2