Rozwiąż nierówność: Dorka: Rozwiąż nierówność: Ix² +1I+1<5

pigor: ..., np. tak: |x²+1|+1|< 5 ⇔ |x²+2|< 5 ⇔ −5< x²+2< 5 /+(−2) ⇔ −7< x²< 3 ⇔ ⇔ x∊R i |x|< √3 ⇔ −√3< x< √3 ⇔ x∊(−√3;√3) . ...

pigor: ... nie źle , rozwiązałem ... inną nierówność , a więc od nowa, np. tak: |x²+1|+1< 5 ⇔ x²+1+1< 5 ⇔ x²+2< 5 ⇔ x²<3 ⇔ |x|<√3 ⇔ ⇔ −√3< x< √3 ⇔ x∊(−√3;√3) i to tyle , koniec . ...

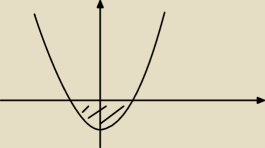
;): możesz opuścić moduł, bo wyrażenie pod nim jest zawsze dodatnie (x²+1 zawsze jest większe od zera) czyli będzie x² +1+1<5 x²+2<5 x²−3<0 (x−√3)x(+√3)<0 miejsca zerowe to √3 i −√3 ramiona funkcji są skierowane do góry przedział którego poszukujemy jest zaznaczony na rysunku z tego wynika, że x∊(−√3;√3)

Dorka: trzeba wyliczyć miejsca zerowe aby sprawdzić czy x zawiera się w danym zbiorze

;): tak też było zrobione w naszych rozwiązaniach z tym, że zapis pigora jest lepszy, bo bardziej zwięzły, a oznacza dokładnie to samo co mój

pigor: ...; ) twój sposób jest bardzo dobry, tylko ten x ("krzyżyk") znaku mnożenia niepotrzebny, bo może być przez niektórych źle zinterpretowany . ...

;): aaa to tego nawet nie zauważyłem teraz dopiero to widze

pigor: ... a więc tam miało być (x−√3)(x+√3)< 0 i wszystko jasne − postać iloczynowa trójmianu kwadratowego . ...