geometria analityczna Andrzej: Dany jest zbiór A={(x,y): x∊R, y∊R oraz x²+y²−4y≤0. Zbiór B jest obrazem zbioru A w translacji o wektor u=[2,−1]. Opisz zbiór B za pomocą nierówności, a następnie zaznacz na płaszczyźnie zbiór (A u B)'. Zbiór B już opisałem, okręgi wyszły mi: O_a: x²+(y−2)²≤4 , O_b: (x−2)²+(y−1)²≤4 tylko mam problem z zaznaczeniem zbioru (AuB)'. Czy nie jest to czasem (AnB)?

Andrzej: Chwileczkę... Zbiorem będzie wszystko oprócz Tych okręgów?

Prometix: (AuB)" to z de morgana jest rowne (A"n B") ten cudzyslow to prim " ( nie moglem znalesc zwyklego znaczka )

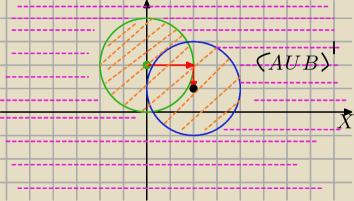
Mila: Dany jest zbiór A={(x,y): x∊R, y∊R oraz x²+y²−4y≤0. x²+(y−2)²−4≤0 x²+(y−2)²≤4 u=[2,−1]. (x−2)²+(y−1)²≤4 (AUB) (AUB)'