wykluczanie zdarzen Ann: Wiadomo, ze B, A ⊂Ω oraz p(a)=1/2 p(b) =2/3 uzasadnij czy zdarzenia moga sie wykluczac wiem, ze wykluczaja sie gdy p(a∪b)=p(a)+p(b) wyszlo mi 7/6 i co dalej?

Eta: Wiesz, że : 0≤P(AUB) ≤1

	7
P(AUB)=		>1
	6

teraz podaj odpowiedź......

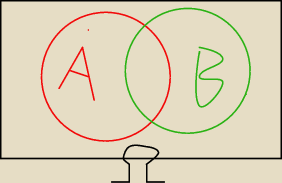Prometix: B,A⊂Ω P(A)=1/2 oraz P(B)=2/3 wiec tak P(AUB)≤1 zawsze, wynika to z wlasnosci prawdopodobienstwa a wiemy ze P(AUB)=P(A)+P(B)−P(AnB) zakladamy ze sie wykluczaja zatem nie maja czexci wspolnej wiec; P(AUB)=1/2+4/3=3/6+4/6=7/6 mamy warunek że P(AUB)≤1 co sie nie zgadza zatem musza miec jakąs czesc wspolną nie ma innej mozliwosci skoro oba sa zawarte w Ω wiec nasze zalozenie jest nieprawdziwe i nie moga sie wykluczac te prawdopodobienstwa

Eta:

Ann: Dziekuje za swietne wytlumaczenie!