.. prosze o pomoc: : Naszkicuj wykres funkcji : f(x) = |4 / (|x|−2) | gdzie x ∈ R – {–2, 2}, a następnie wyznacz wszystkie wartości parametru m, dla których równanie : |4 / (|x|−2) | = 3m – m3 ma cztery rozwiązania

iiiii: f(x)=4/(|x|−2) v f(x)=−4/(|x|−2) z tego masz f(x)= 4/(x−2) dla x>2 oraz f(x)=4/(−x−2)=−4/(x+2) dla x<2 oczywiscie x≠2 i −2 z drugiej alternatywy masz f(x)=−4/(x−2) dla x>2 oraz f(x)=−4/(−x−2)=4/(x+2) dla x <2 oczywiscie x≠2 i −2 i to narusuj

: a w jaki sposob okreslic wartosc parametru m, ? napewno pomoze mi rysunek, ale chyba tez jakie przekstalcenia twgo bym musiala,

Licealista_Theosh: tam jest 3m−m³?

: tak

iiiii: 3m−m³=−m(m²−3m)=−m(m−√3)(m+√3) i teraz to 3m−m³ musi miec 4 rozwiazania patrzysz na jakim to jest przedziale i liczysz np ze 3m−m³>0 i z tego wyliczysz m

: hm, na ktory przedzial patrze?

iiiii: na rysunku zobaczysz na jakim przedziale ma 4 rozwiazania

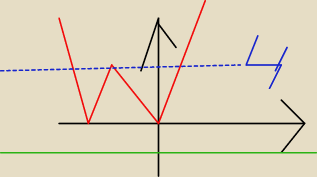
iiiii: z tego przykladowego wykresu wynika ze prosta zielona czyli wlasnie 3m−m³ ma 4 punkty wspolne z tym przykladowym wykresem gdy ; 3m−m³>0 i 3m−m³<4

: na wykresie tego 3m−m³, czy na wykresie tej pierwszje fukcji?

: aha okej, dziekuje

iiiii: nie rysujesz w ogole wykresu 3m−m³ bo to dla jakiegos m da ci stala liczbe wiec ostatecznie to 3m−m³ to bedzie prosta rownolegla do osi ox przykladowo dla liczby m=1 to 3m−m³=2

Mila:

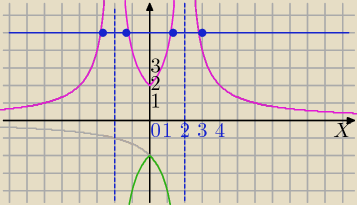
	4
f(x) = |		| gdzie x ∈ R – {–2, 2},
	(|x|−2)

	4
1) y=
	x−2

	4
2) y=
	|x|−2

	4
3) y=|		|
	|x|−2

4 rozwiązania dla y=3m – m³>2⇔ m³−3m+2<0 w(m)=m³−3m+2 = w(1)=1−3+2=0 ⇔ m=1 jest pierwiastkiem wielomianu schemat Hornera: 1 0 −3 2 m=1 1 1 −2 0 m³−3m+2 =(m−1)*(m²+m−2) Δ=9

	−1−3
m=		=−2 lub m=1
	2

m³−3m+2<0⇔(m−1)²*(m*2)<0 i m∊D m<−2