Geometria analityczna Andrzej:

	1
Dane są funkcje f(x)= −x2+2 i g(x)=
	x

a)znajdź punkt o współrzędnych całkowitych w któym przecinają się wykresy f(x) i g(x) b) napisz równania stycznych do wykresów funkcji w tym punkcie c) oblicz tangens kąta przecięcia stycznych a) zrobiłem i jest to punkt (1,1) natomiast nie wiem jak wziąć się za podpunkt b)?

pigor: .., f'(x)= −2x i g'(x)= −¹_x² ⇒ f'(1)= −2= m₁ i g'(1)=−1= m₂ , więc b) s_f : y−1= −2(x−1) ⇔ y=−2x+3 − równanie stycznej do wykresu funkcji f s_g : y−1=−1(x−1) ⇔ y= −x+2 − równanie stycznej do wykresu funkcji g; −−−−−−−−−−−−−−−−−−−−−−−−

	m2−m1		−1+2		1
c) tgα= |		| = |		| =		. ...
	1+m1m2		1+(−1)(−2)		3

Krzysiek : jesli jeszcze pamietam dobrze to styczna do krzywej y=f(x) w punkcie (x_o,f(x_o) ma rownanie y−y_o=f'(x_o)*(x−x_o)

Andrzej: Czy można to zrobić inaczej niż z pochodnych?

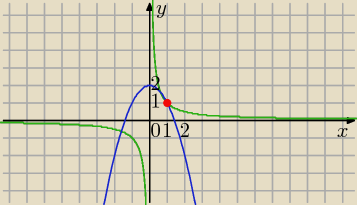
Mila: P=(1,1) − punkt przecięcia wykresów Styczna : s: y=ax+b i (1,1)∊s 1=a*1+b⇔b=1−a s: y=ax+1−a prosta ma mieć jeden punkt wspólny z wykresem funkcji i ...

	1
y=
	x

1
	=ax+1−a⇔
x

ax²+x−ax=1 ax²+x(1−a)−1=0 Δ=(1−a)²+4a=0 a=−1 s: y=−x+2 styczna do hiperboli 2) s1:y=ax+1−a −x²+2=ax+1−a x²+ax−1−a=0 Δ=a²−4*(−1−a)=0 a²+4a+4=0 (a+2)²=0 a=−2 s1: y=−2x+1−(−2) s1: y=−2x+3 styczna do paraboli i kąt jak u Pigora. Trzeba przy tym sposobie odrzucić proste x=1 i y=1