proszę o pomoc w rozwiązaniu tego zadania
Andrzej: f(x)=lx+1l(3−x)
g(x)=lx2−2xl.
muszę znaleźć takie m dla którego funkcja. h(x)=f(x)−g(x)+m. nie ma miejsc zerowych
27 mar 11:55
Artur_z_miasta_Neptuna:
27 mar 11:59
akante: nie kumam
27 mar 12:16
Andrzej: Artur mógłbyś to objasnic
27 mar 12:20
akante: jak "zdjac" te wartosci bezwzgledne? ile przypadkow tu trzeba rozpatrzyc ?

27 mar 12:22
rafal: prosze nich ktos mi pomoze rozwiązac to zadanie
27 mar 14:25
Angrzej: kto jest w stanie rozwiązać to zadanie
27 mar 14:55
Angrzej: i mi pomóc
27 mar 14:56
Mila:
f(x)=lx+1l(3−x)
g(x)=lx
2−2xl.
h(x)=f(x)−g(x)+m
h(x)=|x+1|(3−x)−|x
2−2x|
|x+1|=x+1 dla x≥−1
|x
2−2x|=x
2−2x dla x
2−2x≥0 ⇔x(x−2)≥0⇔x≤0 lub x≥2
Rozważamy wzór h(x) w 4 przedziałach:
1) x<−1
h(x)=(−x−1)(3−x)−(x
2−2x=x
2−2x−3−x
2+2x
h(x)=−3 funkcja stała
2)x∊<−1,0>
h(x)=(x+1)(3−x)−x
2+2x=−x
2+2x+3−x
2+2x
h(x)=−2x
2+4x+3
3) x∊(0,2)
h(x)=(x+1)(3−x)−(−x
2+2x)=−x
2+2x+3+x
2−2x
h(x)=3 funkcja stała,
4) x∊<2,
∞)
h(x)=(x+1)(3−x)−(x
2−2x)=−x
2+2x+3−x
2+2x
h(x)=−2x
2+4x+3
h(x)=f(x)−g(x)+m=0
f(x)−g(x)=−m
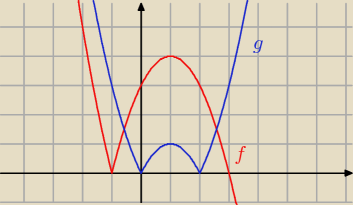
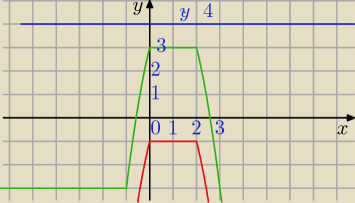
Dla( −m)>3 prosta nie ma punktów przecięcia z wykresem y=f(x)−g(x)
zatem dla m<−3 funkcja h(x) nie ma miejsc zerowych.
Np m=−4
h(x)=f(x)−g(x)−4 wykres czerwony
27 mar 17:18
akante: czemu rozwazalas przedział od 1 do zera i od dwoch do zera zero cos wnosi?

prosze o odpowiedz
28 mar 10:05
Krzysiek : Nie od1 do 0 tylko od < −1 do 0 > i drugie nie od 2 do 0 tylko (0,2) Zobacz .Mila napisala tam
wyzej h(x)=|x+1|(3−x)−|x2−2x|Teraz miejsce zerowe |x+1| jest x=−1 Miejscami zerowymi
|x2−2x| beda x2−2x=x(x−2) to x=0 lub x=2 Masz wyznaczone miejsca zerowe wobec tego mozesz
wyznaczyc przedzialy do rozwiazania tego rownania Wiec tak 1 przedzial bedzie x<−1 (mozesz to
zapisac rowniez jako x∊(−∞,−1) . Drugi przedzial to x∊<−1,0> . Trzeci przedzial to x∊(0,2)
i na koncu 4 przedzial to x∊<2,∞) Rownie dobrze bedzie gdy oznaczysc sobie przedzialy tak
1przedzial x≤−1 inaczej x∊(−∞,−1> 2 przedzial x∊(−1,0> 3 przedzial x∊(0,2> i na koncu
4 prezedzial x∊(2,∞) Osobna sprawa jest tutaj to ze musisz wiedziec w jakim przedziale x2−2x
jest rosnaca a w jakim malejaca gdyz jest to bardzo wazne gdy bedziesz opuszczal |x2−2x|
Zapewne wiesz ze x2−2x>0 w przedziale x∊(−∞,0)U(2,∞) (czyli rosnie ) a w przedziale
x∊(0,2) maleje czyli x2−2x<0
Popatrz teraz na rozwiazanie MIli w poszczegolnych przedzialach i zbacz gdzie zostal zmieniany
znak przy opuszczaniu wartosci bezwzglednej a gdzie nie zostal zmieniony. . Co do rozwazanych
przedzialow to juz chyba wiesz dlaczego .
28 mar 11:09
Mila:
Dziękuję ,Krzysiek za komentarz.
Do autora, popatrz uważnie na (5) i (6) linijkę zapisu, tam napisałam, gdzie opuszczasz znak
wartości bezwzględnej bez zmiany wyrażenia.
28 mar 17:21


 f(x)=lx+1l(3−x)
g(x)=lx2−2xl.
h(x)=f(x)−g(x)+m
h(x)=|x+1|(3−x)−|x2−2x|
|x+1|=x+1 dla x≥−1
|x2−2x|=x2−2x dla x2−2x≥0 ⇔x(x−2)≥0⇔x≤0 lub x≥2
Rozważamy wzór h(x) w 4 przedziałach:
1) x<−1
h(x)=(−x−1)(3−x)−(x2−2x=x2−2x−3−x2+2x
h(x)=−3 funkcja stała
2)x∊<−1,0>
h(x)=(x+1)(3−x)−x2+2x=−x2+2x+3−x2+2x
h(x)=−2x2+4x+3
3) x∊(0,2)
h(x)=(x+1)(3−x)−(−x2+2x)=−x2+2x+3+x2−2x
h(x)=3 funkcja stała,
4) x∊<2,∞)
h(x)=(x+1)(3−x)−(x2−2x)=−x2+2x+3−x2+2x
h(x)=−2x2+4x+3
h(x)=f(x)−g(x)+m=0
f(x)−g(x)=−m
Dla( −m)>3 prosta nie ma punktów przecięcia z wykresem y=f(x)−g(x)
zatem dla m<−3 funkcja h(x) nie ma miejsc zerowych.
Np m=−4
h(x)=f(x)−g(x)−4 wykres czerwony
f(x)=lx+1l(3−x)
g(x)=lx2−2xl.
h(x)=f(x)−g(x)+m
h(x)=|x+1|(3−x)−|x2−2x|
|x+1|=x+1 dla x≥−1
|x2−2x|=x2−2x dla x2−2x≥0 ⇔x(x−2)≥0⇔x≤0 lub x≥2
Rozważamy wzór h(x) w 4 przedziałach:
1) x<−1
h(x)=(−x−1)(3−x)−(x2−2x=x2−2x−3−x2+2x
h(x)=−3 funkcja stała
2)x∊<−1,0>
h(x)=(x+1)(3−x)−x2+2x=−x2+2x+3−x2+2x
h(x)=−2x2+4x+3
3) x∊(0,2)
h(x)=(x+1)(3−x)−(−x2+2x)=−x2+2x+3+x2−2x
h(x)=3 funkcja stała,
4) x∊<2,∞)
h(x)=(x+1)(3−x)−(x2−2x)=−x2+2x+3−x2+2x
h(x)=−2x2+4x+3
h(x)=f(x)−g(x)+m=0
f(x)−g(x)=−m
Dla( −m)>3 prosta nie ma punktów przecięcia z wykresem y=f(x)−g(x)
zatem dla m<−3 funkcja h(x) nie ma miejsc zerowych.
Np m=−4
h(x)=f(x)−g(x)−4 wykres czerwony
 prosze o odpowiedz
prosze o odpowiedz