rysunek do zadania mat123: Na czworościanie foremnym opisano walec w taki sposób , że skośne krawędzie czworościanu są średnicami podstaw walca. znajdż stosunek objętości kuli opisanej na walcu do objętości kuli wpisanej w czworościan. Bardzo prosze o rysunek do zadania

Mila: Mogę Ci wyjaśnić, co masz liczyć, ale rysunek mi nie wychodzi.

Eta: Witaj Mila Trzeba poczekać na mistrza Bogdana

Mila: Witaj Eto, każda próba jest mało przejrzysta, wiem jak to wygląda, ale narysować trudno, już w zeszłym roku to obliczyłam, ale nie narysowałam. Zobaczę co powie Mat123, może jedno denko mu wystarczy do obliczeń? A o drugim opowiem?

dero2005:

	√6
r =		a
	12

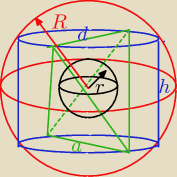
a = d = h

	d√2		a√2
R =		=
	2		2

	R3
k =		= 24√3
	r3

Mila: Dero, trochę inne mam wyniki, może to nieporozumienie z powodu oznaczeń. Widzę to tak: a− krawędź czworościanu, a− średnica walca H_walca= odległości krawędzi skośnych,

	a√2
Hw=
	2

	1		a√6
rkw=		Ho=		promień kuli wpisanej w czworościan
	4		12

Promień kuli opisanej na walcu to połowa przekątnej przekroju osiowego walca

	a√2
p2=(		)2+a2
	2

	3
p2=		a2
	2

	√3		a√6
p=a		=
	√2		2

	a√6
Rko=		−Promień kuli opisanej na walcu
	4

Rko		a√6		a√6		a√6		12
	=		:		=		*		=3
rkw		4		12		4		a√6

	Vk0		33		27
Zatem		=		=
	Vkw		1		1

Eta: odp : 27 jest poprawna

Mila: Dziękuję Eto. Dobranoc.

Eta: Miłych snów

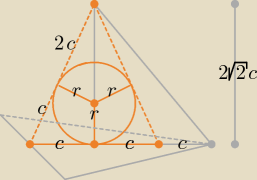
Bogdan: Zostałem wywołany , proponuję w tym zadaniu sporządzić 2 rysunki i zaznaczyć na nich potrzebne do rozwiązania elementy i oznaczenia. Wszystkie długości uzależniam od c. Pole P trójkąta z wpisanym okręgiem o promieniu r (r jest także promieniem kuli wpisanej w czworościan):

	2c + 3c + 3c
P = c*2√2c = 2c2√2 i P =		*r = 4cr ⇒ 4cr = 2c2√2
	2

	c
r =
	√2

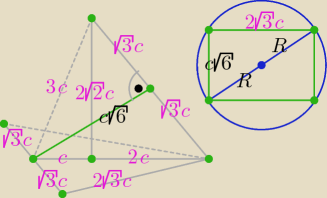
Bogdan: R − długość promienia kuli opisanej na walcu o promieniu podstawy c√3 i wysokości c√6

	3
2R = √18c2 = 3c√2 ⇒ R =		c√2
	2

R		3   c√2 2
	=		= 3
r		c     √2

Stosunek objętości kuli o promieniu R do objętości kuli o promieniu r jest równy

	R
(		)3 = 27
	r

archeolog:

Mila: No, to pięknie, a zainteresowany milczy. Czyli wychodzi na to, że są to promienie kul wpisanych i opisanych na czworościanie. I bez liczenia wynik znany.