Układ równań
bezendu:
Jak rozwiązać taki układ równań ? jakieś wskazówki ?
|x|+|y|=3
2x−y=3
26 mar 21:01
ICSP: rozpisz przedziałami
26 mar 21:02
Licealista_Theosh: Podejrzewam że musisz rozpatrzyć w przedziałach i rozbić to na dwa układy równań.
26 mar 21:03
iiiii: ja bym rozkminil 4 przypadki ( czyli 4 cwiartki )
x<0 i y<0
x<0 i y >0 itd i x oraz y musi nalezec do danej cwiartki w nrozwiazaniu pozmniej bo jak nie
to sprzecznosc

26 mar 21:03
bezendu: czyli 3 przedziały ?
(−∞;0)
<0;1,5)
<1,5;∞)
26 mar 21:05
krystek: 1) x>0i y>0
2)x>0 i y<0
3)x<0i y>0
4x<0 i y<0
26 mar 21:05
ICSP: przypadkami nie przedziałami

Będą 4 przypadki
26 mar 21:05
bezendu: nie rozumiem jakie przypadki
mam z drugiego y=2x−3
|x|+|2x−3|=0 czyli to trzeba chyba rozwiązać jak równanie z wartością bezwzględną

26 mar 21:09
Licealista_Theosh: Ale Y może mieć różne znaki od x. To co napisałeś jest prawdziwe dla jednego przypadku. Zostały
jeszcze 3.
26 mar 21:11
Dominik: musisz rozpatrzyc trzy przypadki (takie jak podala krystek) i w kazdym z nich opuscic znak
wartosci bezwglednej.
np dla przypadku trzeciego (x < 0 ∧ y > 0)
najlatwiej jest te rownania po prostu dodac i od razu wyznaczyc x. nastepnie nalezy sprawdzic
czy spelnia on zalozenie x < 0 i jesli tak to wyznaczyc y (i znowu sprawdzic czy sprawdza
zalozenie, tym razem y > 0). jesli pierwiastki nie spelniaja zalozen nalezy przejsc do
kolejnego przypadku.
26 mar 21:13
bezendu: ok dziękuje
26 mar 21:17
krystek: 1) układ
x+y=3
2x−y=3
__________
2)x−y=3
...
_________
3) −x+y=3
......
__________
4) −x−y=3
...
__________
26 mar 21:24
bezendu:
x+y=3
2x−y=3
x−y=3
2x−y=3
−x+y=3
2x−y=3
−x−y=3
2x−y=3
26 mar 21:31
Mila:
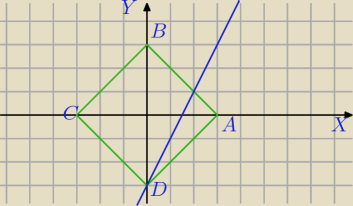
1) graficznie:
|x|+|y|=3 to jest kwadrat o wierzchołkach(3,0)(−3,0)(0,3)(0,−3)
2x−y=3⇔
y=2x−3
Odczytujesz i sprawdzasz
x=0 i y=−3
x=2 i y=1
2) Jeśli niedokładne punkty, to rozwiązujesz równania :
2x−y=3
y=−x+3 równanie prostej AB, podstawiam do pierwszego
2x−(−x+3)=3 ⇔3x=6 ⇔x=2, to y=−2+3=1
para: (2,1)
Drugi układ
2x−y=3 i
y=x−3 równanie prostej AD
2x−(x−3)=3⇔x=0 i y=−3
para:(0,−3)
Metoda algebraiczna
w nowym wpisie, potrzebny rysunek
a)
26 mar 21:31
Mila:
|x|+|y|=3 i 2x−y=3
y=2x−3
|x|+|2x−3|=3
|x|=x dla x≥0
a)
x<0
−x−2x+3=3
−3x=0 ∉(−
∞,0)
x−2x+3=3
−x=0
x=0 i y=−3
x+2x−3=3⇔3x=6⇔x=2
x=2 i y=1
26 mar 21:38
bezendu: czyli na upartego można to zrobić tym drugim sposobem który już mi pokazywałaś ?
26 mar 21:39
Mila:
Co to znaczy na upartego. ( i nie wiem o który sposób Ci chodzi)
Wszystkie podane propozycje są właściwe.
Sposób rozwiązania dostosowujesz do przykładu, rozwiązujesz tym sposobem, który najlepiej
umiesz,i który jest najprostszy, realizujesz polecenia.
W tym przykładzie najlepszy dla mnie ten 21:31 punkt (1).
Podałam kompleksowe rozwiązanie, tu nie było polecenia rozwiązania graficznego.
Zwykle proszą przy takim typie jak pierwsze równanie.
26 mar 21:55
bezendu: czyli żeby od razu zrobić to na przedziały
(−∞;0)
<0;1,5)
<1,5;∞)
26 mar 22:07
Mila: 
26 mar 22:13
bezendu: bez rozpatrywania warunków które podała krystek

a metody graficznej jeszcze nie poznałem ale
podobnież jest łatwiejsza od algebraicznej
26 mar 22:15
Mila:
Krystek podała inny sposób, bardzo pożyteczny w różnych układach z wartością bezwzględną.
Radzę Ci rozwiązać ten układ też tym sposobem. Wtedy wyciągaj wnioski.
26 mar 23:04
bezendu: Ok dziękuję za radę i za szczegółowe opisanie rozwiązania

ale dziś już idę spać więc zrobię
to jutro (mam jeszcze jeden układ do zrobienia) Dobranoc

26 mar 23:11
Mila: Dobranoc, do jutra

26 mar 23:13
bezendu: Hey Mila posłuchałem Twojej rady i zrobiłem ten układ tak jak podała Krystek ale to chyba są
złe
założenia bo w drugim przypadku
2) x>0 i y<0
x−y=3/ (−1)
2x−y=3
−x+y=−3
2x−y=3
x=0
2*0−y=3
y=−3 i to nie należy bo x>0
a U Ciebie w rozwiązaniu jest że para liczb 0,−3 jest rozwiązaniem
więc ja zrobiłem tak : (nie wiem czy dobrze ale własność chyba jest taka |x| = x≥0 −x<0

)
1) x≥0 i y≥0
2) x≥0 i y<0
3) x<0 i y<0
4) x<0 i y ≥0
1) x+y=3
2x−y=3
3x=6/3
x=2
2*2−y=3
−y=−1
y=1
2) x−y=3 /(−1)
2x−y=3
−x+y=−3
2x−y=3
x=0
2*0−y=3
−y=3
y=−3
3) −x−y=3 /(−1)
2x−y=3
x+y−3
2x−y=3
3x=0/3
x=0
2*0−y=3
−y=3
y=−3
4) −x+y=3
2x−y=3
x=6
2*6−y=3
−y=−9
y=9
odp rozwiązaniem układu są pary liczb (2,1) ∨ (0,−3)
27 mar 19:50
Mila: Rozważamy x≥0 lub x<0
y≥0 lub y<0
Dobrze ustawiłeś warunki.
Po rozwiązaniu w poszczególnych punktach odnotuj, że cos nie należy do dziedziny, bo się
pogubisz z odpowiedzią.
Widzisz teraz, że tą metodą sporo liczenia.
Gdy, pod koniec tygodnia będziesz miał czas, to Ci przygotuję przykład na tę metode.
27 mar 20:36
bezendu:
Ok dziękuje

mam jeszcze jedno zadanie z wartością bezwzględną zaraz wstawię
27 mar 20:39
bezendu: Punktom A i B leżącym na osi liczbowej, odpowiadają liczby 3m−4 i m2−m, gdzie m jest pewną
liczbą rzeczywistą. Wyraź odległość punktów A i B w zależności od wartości m
korzystam z |b−a|
|m2−m−(3m−4)|
|m2−m−3m+4|
|m2−4m+4|
|(m−2)2|=(m−2)2
i teraz mogę tak zostawić czy lepiej napisać tą oczywistość (a−b)2≥0 ?
27 mar 20:47
bezendu: ostatni układ już
|x|−y=2
x−|y|=0
1) x≥0 ∧ y≥0
x−y=2
x−y=0
0=2 sprzeczność
2) x≥0 ∧ y<0
x−y=2
x+y=0
2x=2
x=1
1−y=2 x ∊ x≥0
−y=1 y∊ y<0
y=−1
3) x<0 ∧ y<0
−x−y=2
x+y=0
0=2 sprzeczność
4) x<0 ∧ y≥0
−x−y=2
x−y=0
−2y=2/2
−y=1
y=−1 ⊄ y≥0
27 mar 21:10
Mila: Dobrze.
zapisy w punkcie (2)
x∊<0,∞)
y∊(−∞,0) albo
x∊D,y∊D
w punkcie (4)
y∉D albo y∉<0,∞)
28 mar 18:10
bezendu: ok będę pamiętał o tym zapisie

a mogłabyś zobaczyć post z 20:47

28 mar 18:25
Mila: Dobrze masz. Możesz dla świętego spokoju dopisać.
28 mar 18:56
bezendu: Dziękuje

28 mar 18:57
pigor: ... mała uwaga praktyczna do rozwiązania układu powyżej : otóż
warto zauważyć, że może być tylko x≥0 ( odpada więc przypadek x<0),
bo po przekształceniu mamy kolejno
|x|−y=2 i x−|y|=0 ⇔ |y|=x i x≥0 (z definicji modułu) i |x|=y+2 i y+2 ≥0 wtedy ⇔
⇔ (y=−x lub y=x) i x ≥0 i (x=−x+2 lub x=x+2) i y >−2 ⇔ (x=1 lub 0=2) i y=−1 ⇔
⇔
(x,y)=(1,−1) i koniec . ...

28 mar 20:30
bezendu: czemu odpada x<0 ?
28 mar 20:33
pigor: .. , czyżbyś nie czytał że zrozumieniem

tu właśnie wyjaśniam "|y|=x i x≥0 (z definicji modułu)" , bo gdyby było x<0 to
równość |y|=x nie miałaby sensu właśnie z definicji modułu (wartości bezwzględnej liczby)
28 mar 20:40
bezendu: ok dziękuję
28 mar 20:48
Mila: Tak, do każdego zadania należy podchodzić indywidualnie.
To, co zauważył Pigor, często ułatwia i skraca rozwiązanie.
Warto zobaczyć, jak wygląda sytuacja, gdy dokonamy przekształcenia.
28 mar 20:51
bezendu: ale chyba błędem nie jest że nie zrobię tego przekształcenia co
Pigor tylko policzę tym
sposobem co podała
Krystek 
28 mar 20:59
Mila: Napisałam Ci, że dobrze jest, ale uwaga jest bardzo cenna, bo skraca rozwiązanie.
28 mar 21:02
pigor: ... i właśnie o to "skracanie" każdego rozwiązania mi chodzi, bo czas to
pieniądz zwłaszcza na ... ograniczonym w czasie egzaminie, maturze .itp. ...

28 mar 21:06

 Będą 4 przypadki
Będą 4 przypadki

 1) graficznie:
|x|+|y|=3 to jest kwadrat o wierzchołkach(3,0)(−3,0)(0,3)(0,−3)
2x−y=3⇔y=2x−3
Odczytujesz i sprawdzasz
x=0 i y=−3
x=2 i y=1
2) Jeśli niedokładne punkty, to rozwiązujesz równania :
2x−y=3
y=−x+3 równanie prostej AB, podstawiam do pierwszego
2x−(−x+3)=3 ⇔3x=6 ⇔x=2, to y=−2+3=1
para: (2,1)
Drugi układ
2x−y=3 i y=x−3 równanie prostej AD
2x−(x−3)=3⇔x=0 i y=−3
para:(0,−3)
Metoda algebraiczna
w nowym wpisie, potrzebny rysunek
a)
1) graficznie:
|x|+|y|=3 to jest kwadrat o wierzchołkach(3,0)(−3,0)(0,3)(0,−3)
2x−y=3⇔y=2x−3
Odczytujesz i sprawdzasz
x=0 i y=−3
x=2 i y=1
2) Jeśli niedokładne punkty, to rozwiązujesz równania :
2x−y=3
y=−x+3 równanie prostej AB, podstawiam do pierwszego
2x−(−x+3)=3 ⇔3x=6 ⇔x=2, to y=−2+3=1
para: (2,1)
Drugi układ
2x−y=3 i y=x−3 równanie prostej AD
2x−(x−3)=3⇔x=0 i y=−3
para:(0,−3)
Metoda algebraiczna
w nowym wpisie, potrzebny rysunek
a)
 |x|+|y|=3 i 2x−y=3
y=2x−3
|x|+|2x−3|=3
|x|=x dla x≥0
|x|+|y|=3 i 2x−y=3
y=2x−3
|x|+|2x−3|=3
|x|=x dla x≥0

 a metody graficznej jeszcze nie poznałem ale
podobnież jest łatwiejsza od algebraicznej
a metody graficznej jeszcze nie poznałem ale
podobnież jest łatwiejsza od algebraicznej
 ale dziś już idę spać więc zrobię
to jutro (mam jeszcze jeden układ do zrobienia) Dobranoc
ale dziś już idę spać więc zrobię
to jutro (mam jeszcze jeden układ do zrobienia) Dobranoc 

 )
1) x≥0 i y≥0
2) x≥0 i y<0
3) x<0 i y<0
4) x<0 i y ≥0
1) x+y=3
2x−y=3
3x=6/3
x=2
2*2−y=3
−y=−1
y=1
2) x−y=3 /(−1)
2x−y=3
−x+y=−3
2x−y=3
x=0
2*0−y=3
−y=3
y=−3
3) −x−y=3 /(−1)
2x−y=3
x+y−3
2x−y=3
3x=0/3
x=0
2*0−y=3
−y=3
y=−3
4) −x+y=3
2x−y=3
x=6
2*6−y=3
−y=−9
y=9
odp rozwiązaniem układu są pary liczb (2,1) ∨ (0,−3)
)
1) x≥0 i y≥0
2) x≥0 i y<0
3) x<0 i y<0
4) x<0 i y ≥0
1) x+y=3
2x−y=3
3x=6/3
x=2
2*2−y=3
−y=−1
y=1
2) x−y=3 /(−1)
2x−y=3
−x+y=−3
2x−y=3
x=0
2*0−y=3
−y=3
y=−3
3) −x−y=3 /(−1)
2x−y=3
x+y−3
2x−y=3
3x=0/3
x=0
2*0−y=3
−y=3
y=−3
4) −x+y=3
2x−y=3
x=6
2*6−y=3
−y=−9
y=9
odp rozwiązaniem układu są pary liczb (2,1) ∨ (0,−3)
 mam jeszcze jedno zadanie z wartością bezwzględną zaraz wstawię
mam jeszcze jedno zadanie z wartością bezwzględną zaraz wstawię
 a mogłabyś zobaczyć post z 20:47
a mogłabyś zobaczyć post z 20:47 


 tu właśnie wyjaśniam "|y|=x i x≥0 (z definicji modułu)" , bo gdyby było x<0 to
równość |y|=x nie miałaby sensu właśnie z definicji modułu (wartości bezwzględnej liczby)
tu właśnie wyjaśniam "|y|=x i x≥0 (z definicji modułu)" , bo gdyby było x<0 to
równość |y|=x nie miałaby sensu właśnie z definicji modułu (wartości bezwzględnej liczby)

