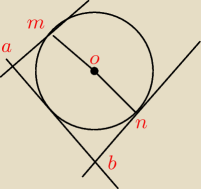
zad ...: Odcinek MN jest średnicą okręgu o(O, r), gdzie r = 2. Proste m i n są styczne do okręgu odpowiednio w punktach M oraz N. Przez punkt P okręgu, który nie należy do średnicy MN, poprowadzono styczną p, przecinającą proste m i n odpowiednio w punktach A i B (zobacz rysunek). a) Wykaż, że |AOB| = 90°. b) Oblicz wartość iloczynu |AP| ⋅ |PB|n

...: bez tego "n" na koncu w b)

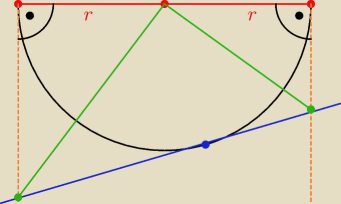
Artur_z_miasta_Neptuna: zauważmy że styczne przechodzące przez m i n są do siebie równoległe stąd ... trzy styczne + średnica okręgu tworzą trapez prostokątny

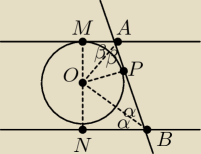
irena_1: a) Czworokąt MNBA to trapez równoramienny. Suma kątów NBA i BAM jest kątem półpełnym Trójkąty MOA i OPA oraz trójkąty ONB i OBP to pary trójkątów przystających, czyli kąty α i β dają w sumie kąt prosty. W trójkącie AOB kąt AOB jest kątem prostym

irena_1: b) Trójkąt AOB jest prostokątny, AB to przeciwprostokątna, OP to wysokość trójkąta poprowadzona na przeciwprostokątną. |AP|*|PB|=|OP|²=2²=4

...: a skad wiemy ze jest to trapez rownoramienny, i skad wiemy ze tam sa te same katy β i α?

irena_1: a) Oczywiście− trapez prostokątny, nie równoramienny (dopiero teraz zobaczyłam, co zapisałam)

...: jest to trapez prostokatny, nie rownoramienny, tylko zastanawiam sie skad wiesz o tych katach z jakich wlasnosci tam dales dwie α iβ

...:

irena_1: Trójkąty NBO i PBO to trójkąty prostokątne mające wspólną przeciwprostokątną i równe przyprostokątne ON i OP (promienie okręgu). Są więc przystające.

...: maja rowną jedno przyprostokatną która jest promieniem maja wspolnu kat 90 i przeciwporstokatna czylyi zwlasnosci bkb?

irena_1: Jeśli mają równą przeciwprostokątną i jedne z przyprostokątnych, to drugie przyprostokątne też muszą być równe (twierdzenie Pitagorasa). Cecha (bbb)

...: no tak, zacmienie chwilowe.

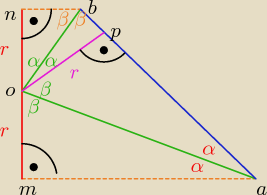
Artur_z_miasta_Neptuna: a więc mamy: 1) zauważamy, że: Δoma = Δ opa (podobieństwo − bok, bok, kąt) stąd mamy kąty α jak również Δobn = Δobp (to samo podobieństwo) −−− tylko na rysunku tego nie widać stąd mamy kąty β 2) jest to trapez, a więc suma kątów wewnętrznych = 360 90+90 + 2β + 2α = 360 → α+β=90 → α = 90−β i stąd mamy kąty na zielono jak widzisz mamy że kąt aob = α+β = 90^o c.n.w.

...: dzieki wam