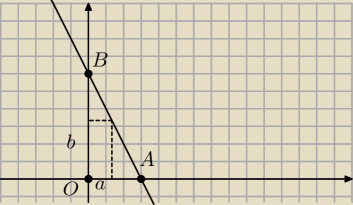
 Prosta o równaniu y=6−2x wraz z osiami układu współrzędnych wyznacza trójkąt prostokątny ABO.
W trójkąt ten wpisano prostokąt w ten sposób, że jeden z wierzchołków prostokąta znajduje się
w początku układu współrzędnych a dwa inne na osiach układu współrzędnych. Czwarty wierzchołek
leży na odcinku AB. Uzasadnij, że pole tego prostokąta nie jest większe od połowy pola
trójkąta ABO.
A=(3,0)
B=(6,0)
b=6−2a
PΔ = 9
mógłby mi ktoś powiedzieć co mam dalej zrobić?
z góry dziękuje za pomoc
Prosta o równaniu y=6−2x wraz z osiami układu współrzędnych wyznacza trójkąt prostokątny ABO.
W trójkąt ten wpisano prostokąt w ten sposób, że jeden z wierzchołków prostokąta znajduje się
w początku układu współrzędnych a dwa inne na osiach układu współrzędnych. Czwarty wierzchołek
leży na odcinku AB. Uzasadnij, że pole tego prostokąta nie jest większe od połowy pola
trójkąta ABO.
A=(3,0)
B=(6,0)
b=6−2a
PΔ = 9
mógłby mi ktoś powiedzieć co mam dalej zrobić?
z góry dziękuje za pomoc 

 a(6−2a) ≤ 4,5
−4a2 + 12a − 9 ≤ 0
Δ=0
a=3/2
a ≥ 3/2
a(6−2a) ≤ 4,5
−4a2 + 12a − 9 ≤ 0
Δ=0
a=3/2
a ≥ 3/2
| −36 | ||
max=q= | =4<4,5 | |
| −8 |