Oblicz pole pierścienia kołowego grzegorz.f-16: Dane są dwa współśrodkowe okręgi o różnych promieniach. Cięciwa większego okręgu styczna do mniejszego okręgu ma długość 18. Oblicz pole pierścienia kołowego utworzonego przez te okręgi. (Pierścień kołowy, to część płaszczyzny ograniczona dwoma okręgami).

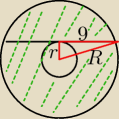
irena_1: Pole pierścienia: P_p=πR²−πr²=π(R²−r²) Z tego trójkąta prostokątnego r²+9²=R²\\R²−r²=81 P_p=81π

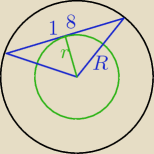
dero2005: R = √9² + r² = √81 + r² S = πR² − πr² = π(R² − r²} = π(81 + r² − r²) = 81π