f(x) Citizen: http://d.naszemiasto.pl/k/r/37/7d/50e71392a5479_o.jpg zrobiłem podpunkty 1 i 2 tak jak na rozwiązaniu , ale nie wiem jak ten ktoś narysował wykres i skąd wziął taki przedział w odpowiedzi , pilne

jikA:

	⎧	x ; x ≥ a
|x − a| =	⎨
	⎩	−x ; x < a

Citizen: znam ten wzór na wartości bezwzględne , moje pytanie brzmi : otrzymałem dwie funkcje , f(x)=−2x+3 . f(x)=−2x−3 jak narysować te dwa wykresy tak jak na rozwiązaniu , próbowałem tabelki , ale wyszło podobnie , ale innaczej , i skąd wzią się przedział w odpowiedzi (−&,−7)u(−1,+&)

jikA: Dla x < 2 rysujesz wykres funkcji f(x) = −2x + 3 natomiast dla x > 2 rysujesz wykres funkcji f(x) = −2x − 3.

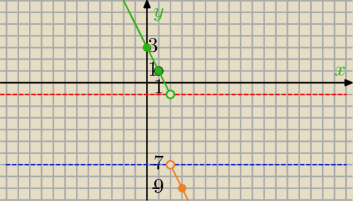
Mila: 1) Wykres funkcji liniowej; (lewy) f(x)=−2x+3 dla x∊(−∞,2) f(0)=3 f(1)=−2+3=1 2) wykres funkcji liniowej ( prawy− dolny) f(x)=−2x−3 dla x∊(2,∞) f(3)=−2*3−3= −6−3=−9 f(4)=−2*4−3 3) Zbiór wartości odczytujesz na osi OY Od czerwonej przerywanej w górę i od niebieskiej w dół. y∊(−∞,−7)U(−1,∞)

Citizen: piękny rysunek , zrobiłem tak: 1) f(x)=−2x+3 f(1)=1 f(1.5)=0 2) f(3)=−9 f(4)=−11 3) czyli xe(−∞,−9)U(0,+∞) , podstawiłem dowolne x spełniające założenia , czy moje rozwiązanie też jest dobre

Mila: Dobrze policzyłeś punkty wykresu Zbiór wartości źle, Nie ponieważ graniczne punkty to (2,−1) oraz (2,−7) ale masz kółka otwarte, bo 2 nie należy do dziedziny, jednak prosta dochodzi do tego punktu. Podobnie z drugą funkcją. Przeczytaj co Ci napisałam w punkcie (3).

Citizen: czego u cb jest −7 , jak wyznaczyłaś te linie czerwoną i niebieską?

Mila: Właściwie to możesz liczyć dla obu funkcji f(2) i kółko ma być otwarte.

Citizen: już rozumiem Mila,fajny kolorek,wiosenny, dziękuję za pomoc

Mila: