 )
Korzystam ze wzoru P(A\B)=P(A∩B) : P(B)
Czyli P(A∩B)=P(A\B)*P(B)=0,3*0,4=0,12
Zdarzenia się niezależne jeśli
P(A∩B)=P(A)*P(B)
0,12=(?)0,5*0,4
0,12=(?)0,2
widać że nie, czyli są zależne.
A w odpowiedzi jest: "Są niezależne". Gdzie jest błąd?
Z góry dziękuję za odpowiedź.
Pozdrawiam
)
Korzystam ze wzoru P(A\B)=P(A∩B) : P(B)
Czyli P(A∩B)=P(A\B)*P(B)=0,3*0,4=0,12
Zdarzenia się niezależne jeśli
P(A∩B)=P(A)*P(B)
0,12=(?)0,5*0,4
0,12=(?)0,2
widać że nie, czyli są zależne.
A w odpowiedzi jest: "Są niezależne". Gdzie jest błąd?
Z góry dziękuję za odpowiedź.
Pozdrawiam
| P(A∩B) | ||
P(A\B) ≠ P(A|B) = | ||
| P(B) |
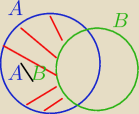 A\B= A\ (A∩B)
to: P(A)−P(A∩B)= 0,3 ⇒ P(A∩B)= 0,2
Jeżeli P(A∩B)= P(A)*P(B) to zdarzenia A i B są niezależne
dokończ.........
A\B= A\ (A∩B)
to: P(A)−P(A∩B)= 0,3 ⇒ P(A∩B)= 0,2
Jeżeli P(A∩B)= P(A)*P(B) to zdarzenia A i B są niezależne
dokończ.........
 Artur: Widać źle zrozumiałem | a \ i wyszło mi że jest to to samo, a jak widać nie jest
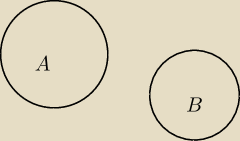
Eta: A skąd wiesz że nie będą rozłączne, czyli:
Artur: Widać źle zrozumiałem | a \ i wyszło mi że jest to to samo, a jak widać nie jest
Eta: A skąd wiesz że nie będą rozłączne, czyli: