trójkąt wpisany w okrąg
Marta: Trójkąt ABC wpisany jest w okrąg o środku O. Oblicz miarę kąta AOB jeżeli
a) |<BAC|=80 stopni |<AOC|=140 stopni
b) |<ABC|=50 stopni i |AB|=|BC|
c) trójkąt jest równoramienny i dwusieczna kąta przy podstawie AB tworzy z przeciwległym bokiem
kąt o mierze 60 stopni
25 mar 14:12
gosia:
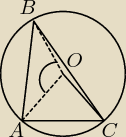
Rysunek trochę prowizoryczny ale widać co trzeba

a)
∡BAC=80
∡AOC=140 jest to kąt środkowy oparty na tym samym łuku co kąt wpisany ∡ABC
Zasada jest taka że środkowy ma 2 razy więcej niż wpisany zatem
∡ABC=70
Suma wszystkim kątów w trójkącie jest równa 180:
∡ABC+∡BAC+∡BCA=180
70+80+∡BCA=180
∡BCA=30
∡BCA jest kątem wpisanym opartym na tym samym łuku co nasz szukany kąt ∡AOB
2x∡BCA=∡AOB
2x30=60 jest to miara ∡AOB
25 mar 15:46
pigor: ...., z tw. o kątach wpisanych i środkowych okręgu
a)
|∡AOB|= 360
o−140
o−2*80
o= 360
o−300
o=
60o ,
b) 2|∡AOB|+2*50
o= 360
o ⇔ 2|∡AOB|= 260
o ⇒
∡AOB|=130o ,
c) niech α − miara kąta dwusiecznej z AB, to z warunków zadania :
α+2α+60
o=180
o ⇒ 3α= 120
o ⇒
α=40o , więc np
|∡AOB=| 2|∡ACB|= 2(6
o−α)= 2(60
o−40
o)=
40o . ...

25 mar 16:09
gosia:
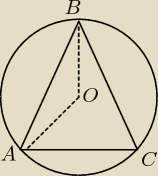
b)
∡ABC=50
|AB|=|BC| skoro trójkąt jest równoramienny to kąty ∡BAC i ∡BCA mają taką samą miarę
∡ABC+∡BAC+∡BCA=180
50+∡BAC+∡BCA=180
50+2x∡BAC=180
2x∡BAC=130
∡BAC=65
kąt ∡AOB jest środkowy oparty na łuku ∡BCA
∡AOB=2x∡BCA=130
25 mar 16:12
Martaa: co do podpunktu C to skąd wiadomo ze <ACB=(60−α) oraz α+2α+60=180 skąd to 2α
25 mar 17:45
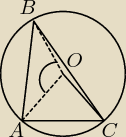 Rysunek trochę prowizoryczny ale widać co trzeba
Rysunek trochę prowizoryczny ale widać co trzeba a)
∡BAC=80
∡AOC=140 jest to kąt środkowy oparty na tym samym łuku co kąt wpisany ∡ABC
Zasada jest taka że środkowy ma 2 razy więcej niż wpisany zatem
∡ABC=70
Suma wszystkim kątów w trójkącie jest równa 180:
∡ABC+∡BAC+∡BCA=180
70+80+∡BCA=180
∡BCA=30
∡BCA jest kątem wpisanym opartym na tym samym łuku co nasz szukany kąt ∡AOB
2x∡BCA=∡AOB
2x30=60 jest to miara ∡AOB
a)
∡BAC=80
∡AOC=140 jest to kąt środkowy oparty na tym samym łuku co kąt wpisany ∡ABC
Zasada jest taka że środkowy ma 2 razy więcej niż wpisany zatem
∡ABC=70
Suma wszystkim kątów w trójkącie jest równa 180:
∡ABC+∡BAC+∡BCA=180
70+80+∡BCA=180
∡BCA=30
∡BCA jest kątem wpisanym opartym na tym samym łuku co nasz szukany kąt ∡AOB
2x∡BCA=∡AOB
2x30=60 jest to miara ∡AOB

 b)
∡ABC=50
|AB|=|BC| skoro trójkąt jest równoramienny to kąty ∡BAC i ∡BCA mają taką samą miarę
∡ABC+∡BAC+∡BCA=180
50+∡BAC+∡BCA=180
50+2x∡BAC=180
2x∡BAC=130
∡BAC=65
kąt ∡AOB jest środkowy oparty na łuku ∡BCA
∡AOB=2x∡BCA=130
b)
∡ABC=50
|AB|=|BC| skoro trójkąt jest równoramienny to kąty ∡BAC i ∡BCA mają taką samą miarę
∡ABC+∡BAC+∡BCA=180
50+∡BAC+∡BCA=180
50+2x∡BAC=180
2x∡BAC=130
∡BAC=65
kąt ∡AOB jest środkowy oparty na łuku ∡BCA
∡AOB=2x∡BCA=130