| 3 | ||
wewnętrznych równa się | . | |
| 8 |
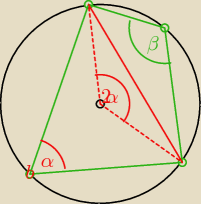 a twierdzenia cosinusów wyznaczysz 2α .... czyli i kąt α .... czyli i β jako 180−α
... i tak dalej −
a twierdzenia cosinusów wyznaczysz 2α .... czyli i kąt α .... czyli i β jako 180−α
... i tak dalej −
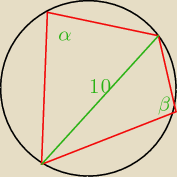 Można tez twierdzeniem sinusów.
β = 180 − α
Można tez twierdzeniem sinusów.
β = 180 − α
| 10 | |
= 10√2 | |
| sinα |
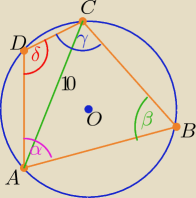 Z warunku wpisania czworokąta w okrąg
α+γ=180o = β+δ
sinγ= sin(180o−α)= sinα podobnie sinδ= sinβ
Z warunku wpisania czworokąta w okrąg
α+γ=180o = β+δ
sinγ= sin(180o−α)= sinα podobnie sinδ= sinβ
| 3 | ||
z treści zadania : sinα*sinγ*sinβ*sinδ= sin2α*sin2β= | ||
| 8 |
| √3 | √3 | √2 | ||||
to sinα*sinβ= | = | * | ||||
| 2√2 | 2 | 2 |
| 10 | ||
sprawdzamy czy : w Δ ABC ze wzoru sinusów | = 2R | |
| sin45o |
| 20 | ||
= 10√2 −−− zachodzi | ||
| √2 |
| 10 | ||
i | = 2R ... też zachodzi | |
| sin135o |