Równanie osi symetrii kwadratu Pszemek: Mam punkty: A=(−2,0) B=(1,1) C=(0,4) D=(−3,3) są one kolejnymi wierzchołkami kwadratu. Środek symetrii kwadratu to (−1,2) i mam wielki problem z określeniem równania osi symetrii tego kwadratu. Czytałem, coś próbowałem i coś mi tu nie wychodzi, dlatego proszę was o pomoc, byście zrobili mi to rownanie. Będę wdzięczny.

Dominik: umiesz wyznaczyc rownanie prostej przechodzacej przez dwa punkty?

Pszemek: no tak, czyli mam to zrobić z ab i cd?

Dominik: wyznacz zatem proste AB i BC (albo CD i AD). ile jest osi symetrii kwadratu? jak one maja sie do bokow kwadratu (jest moze jakas zaleznosc?)?

krystek:

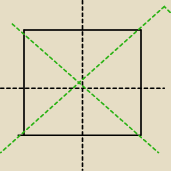
Pszemek: 4 osie, przekątne i proste równoległe do boków kwadratu i przechodzą przez środki pozostałych boków a i pytanie kolejne, później, po wyznaczeniu tych równań mam obliczyć r okręgu wpisanego i opisanego, skąd wówczas mam wziąć długość r?

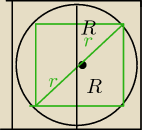
Dominik: a − dlugosc boku kwadratu r − dlugosc promienia okregu wpisanego w kwadrat R − dlugosc promienia okregu opisanego na kwadracie

	a
r =
	2

	a√2
R =
	2

Pszemek: no tak, to wiem, ale skąd mam wziąć a w takim razie (pomyliło mi się )

krystek:

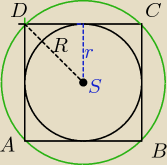
Pszemek: krystek, to też wiem w sensie, długość a mam obliczyć z długości odcinka chociażby ab?

Dominik: dokladnie

krystek:

Pszemek: dobra, dzięki wielkie

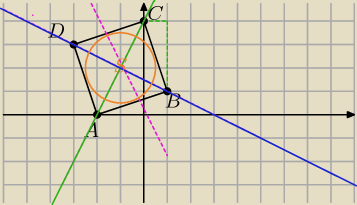
Mila: A=(−2,0) B=(1,1) C=(0,4) D=(−3,3) Osie symetrii: AC: y=ax+b ,b=4 ponieważ prosta przecina oś OY w punkcie (0,4) y=ax+4 i 0=−2a+4⇔a=2 AC: y=2x+4 DB⊥AC

	1		1		3
DB: y=−		x+b i 1=−		*1+b ⇔b=
	2		2		2

	1		3
DB: y=−		x+
	2		2

środek AB:

	−3		1
P1=(		,		)
	2		2

Srodek DC:

	−3		7
P2=(		,		)
	2		2

napisz równanie osi symetrii przechodzącej przez środki boków, a potem pozostaje Ci jedna oś a=√1²+3²=√10

	1
r=		√10 S=(−1,2)
	2

	1
(x+1)2+(y−2)2=(		√10 )2
	2

	10
(x+1)2+(y−2)2=
	4

	1
R=		*√10√2 dokończ.
	2