 c=2R
c2=132+122=169+144=313
c=√313
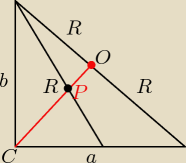
R− promień okręgu opisanego na tym trójkącie (średnicą jest przeciwprostokątna)
P− środek ciężkości (punkt przecięcia środkowych)
c=2R
c2=132+122=169+144=313
c=√313
R− promień okręgu opisanego na tym trójkącie (średnicą jest przeciwprostokątna)
P− środek ciężkości (punkt przecięcia środkowych)
| c | √313 | |||
|CO|=R= | = | |||
| 2 | 2 |
| 2 | 2 | √313 | √313 | |||||
|CP|= | *|CO|= | * | = | |||||
| 3 | 3 | 2 | 3 |
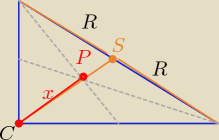 c −− długość przeciwprostokątnej
c=2R , R−− dł. promienia okręgu opisanego na trójkącie prostokątnym
c −− długość przeciwprostokątnej
c=2R , R−− dł. promienia okręgu opisanego na trójkącie prostokątnym
| 1 | ||
|CS|=R= | c | |
| 2 |
| 2 | c | 1 | ||||
x= | * | = | c=....... | |||
| 3 | 2 | 3 |
