zadania zadanie: Podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC , w którym |AB | = 30 , |BC | = |AC | = 3 9 i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka S ma długość 26. Oblicz objętość tego ostrosłupa. skad mam wiedziec ze spodek wysokosci ostroslupa jest srodkiem okregu wpisanego w podstawe?

irena_1: Jeśli wszystkie wysokości ścian bocznych ostrosłupa są równe (lub jeśli wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod takim samy kątem), to spodek wysokości ostrosłupa jest środkiem okręgu wpisanego w podstawę. Tak jest, bo wtedy spodek wysokości jest równo odległy od wszystkich boków podstawy.

irena_1: p− połowa obwodu

	39+39+30
p=		=54
	2

54−39=15 54−30=24 P=√54*15²*24=540 P=pr 54r=540 r=10 H²=26%2−10²=676−100=576 H=24

	1
V=		*540*24=4320
	3

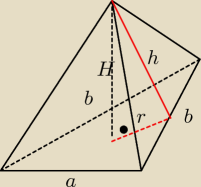
irena_1: a=30 b=39 h=26

zadanie: dziekuje