Oblicz promień okręgu opisanego na trapezie damorka: Dobry wieczór mam problem z takim zadankiem: W trapezie równoramiennym ABCD długości podstaw są równe |AB|= 5 i |CD|= 3. Oblicz promień okręgu opisanego na tym trapezie, jeśli: a) wysokość trapezu jest równa 3, b) kąt ostry trapezu jest równy 30st. Narysowałam ten trapez i okrąg na nim opisany i... utknęłam w martwym punkcie... nie wiem jak ugryźć to zadanko. Mógłby ktoś być tak miły i mnie jakoś nakierować? Z góry dziękuję

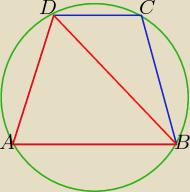Bogdan: Wskazówki: Okrąg opisany na trapezie ABCD jest jednocześnie okręgiem opisanym na trójkącie ABD lub na trójkącie BCD. Dla wyznaczenia długości promienia okręgu opisanego na trapezie wystarczy wyznaczyć długość promienia okręgu opisanego na jednym z tych trójkątów.

	abc		a		b		c
Przypominam, że R =		oraz		=		=		= 2R,
	4PΔ		sinα		sinβ		sinγ

gdzie: R − długość promienia okręgu opisanego na trójkącie, a, b, c − długości boków trójkąta, α, β, γ − miary kątów wewnętrznych trójkąta, P_Δ − pole powierzchni trójkąta.

damorka: Dziękuję bardzo teraz to już bez problemu rozwiążę