Suma długości boków trójkąta równoramiennego Ted: Suma długości boków trójkąta równoramiennego wynosi 24. Jaką długość powinna mieć podstawa trójkąta, aby po obrocie trójkąta wokół niej, uzyskać bryłę o możliwie największej objętości? Wzór na stożek: 1/3 π r² H Z treści zadania mamy: 24 = 2x + 2r Czyli, aby uzyskać bryłę o jak największej objętości szukamy jak największego promienia (ponieważ ten parametr we wzorze rośnie najbardziej) Próbowałem się bawić w zapisywanie warunku istnienia trójkąta i szukanie w tym warunku jak największego r, ale nie wychodziło

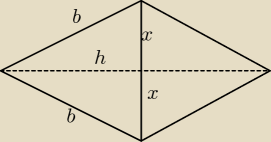irena_1: a=2x 2x+2b=24 x+b=12 b=12−x h²=b²−x²=(12−x)²−x²=144−24x

	1		2
V=2*		*h2*x=		π*24(6−x)*x=16πx(6−x)
	3		3

0<x<6

	0+6
xw=		=3
	2

a=6

Ted: No tak. Czytanie ze zrozumieniem Dziękuję.