Okręgi zadanie typy Wykaż
mmm: Dwa okręgi o różnych promieniach przecinają się w punktach P i Q. Odcinek QA jest średnicą
pierwszego okręgu, za QB− średnicą drugiego okręgu. Wykaż, że punkty A, P, B są współliniowe

nie wiem jak to rozwiązać z rysunku to wynika ale jak to uzasadnić
24 mar 16:08
Eta:
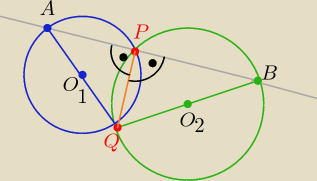
24 mar 16:33
mmm:
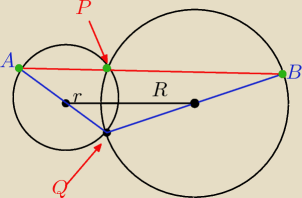
Q
24 mar 16:35
mmm: Dzięki ubiegłąś mnie z rysunkiem
24 mar 16:35
mmm: Ale jak to uzasadnić bo sam rysunek to za mało
24 mar 16:36
Eta:
|∡APQ|=90
o i |∡BPQ|= 90
o (myślę,że wiesz dlaczego? .. napisz to w komentarzu
to |∡APB|=180
o ⇒ punkty A,P,B należą do prostej AB
zatem są współliniowe

24 mar 17:00
mmm: ok dzięki ale ja dziś nie myśle 90 +90 to 180 Więc muszą być wspóliniowe ja próbowałem i
szukałem jakiś zależności promieni
24 mar 17:04
 nie wiem jak to rozwiązać z rysunku to wynika ale jak to uzasadnić
nie wiem jak to rozwiązać z rysunku to wynika ale jak to uzasadnić

 Q
Q
