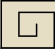
 Długosc odcinków , z których składa sie spirala (rysunek obok), tworza ciag geometryczny o
ilorazie q=0,9. Uzasadnij,że jeśli najdłuzszy z odcinków ma długosc 2, to suma długosci
dowolnej liczby poczatkowych odcinków tej spirali jest mniejsza od 20. Jeśli jest ktoś na
tyle
dobry z matematyki alby to zrobić prosze rówinież o dokładne WYTŁUMACZENIE
Długosc odcinków , z których składa sie spirala (rysunek obok), tworza ciag geometryczny o
ilorazie q=0,9. Uzasadnij,że jeśli najdłuzszy z odcinków ma długosc 2, to suma długosci
dowolnej liczby poczatkowych odcinków tej spirali jest mniejsza od 20. Jeśli jest ktoś na
tyle
dobry z matematyki alby to zrobić prosze rówinież o dokładne WYTŁUMACZENIE
| 1 | 2 | |||
S= | = | =20 | ||
| 1−0,9 | 0,1 |
| 1−0,9n | ||
Ł=2* | =20*(1−0,9n) | |
| 1−0,9 |