Chyba twierdzenie sinusów?
parasol:
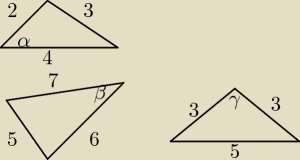
Nie mam pojęcia jak mam to policzyć tylko z długości boków... pomóżcie...
24 mar 14:21
Kaja: spróbuj policzyć z tw. cosinusów
24 mar 14:22
parasol: a2=b2+c2−2*b*c*cosα
a2/cosα=b2+c2−2*b*c
9/cosα=4+16−2*4*2
9/cosα=20−16
9/cosα=4
9=4cosα
cosα=9/4
co dalej?
24 mar 14:27
irena_1:
4
2=2
2+3
2−2*2*3cosα
16=4+9−12cosα
12cosα=−3
cosinus jest równy 0,25 dla kąta około 75
0, więc α ≈ 180
0−75
0=105
0
24 mar 15:04
irena_1:
Źle zaznaczyłam sobie kąt, przepraszam.
Powinno być:
3
2=4
2+2
2−2*4*2cosα
9=16+4−16cosα
16cosα=11
α ≈ 47
0
24 mar 15:06
parasol: dzięki
24 mar 15:10
irena_1:
5
2=7
2+6
2−2*7*6cosβ
25=49+36−84cosβ
84cosβ=60
β ≈ 44
0
24 mar 15:14
irena_1:
5
2=2*3
2−2*3
2cosγ
25=18−18cosγ
18cosγ=−7
Z tablic odczytujesz cosinus− kąt około 67
0
γ ≈ 180
0−67
0=113
0
24 mar 15:16
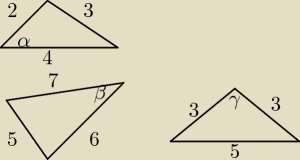 Nie mam pojęcia jak mam to policzyć tylko z długości boków... pomóżcie...
Nie mam pojęcia jak mam to policzyć tylko z długości boków... pomóżcie...