Pole trójkąta Pati: Oblicz pole trójkąta ABC, jeżeli: |AC|= 4, |AB|= 7, kąt BAC = 60 stopni

tim: Jakie znasz wzorY na pole trójkąta?

Pati: 1/2 *a *h, na dowolny trójkąt.( wzór herona)

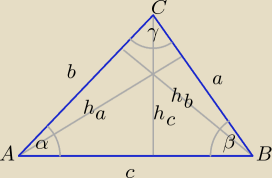
Bogdan: Trzeba wiedzieć, że pole powierzchni dowolnego trójkąta można obliczyć z następujących wzorów:

	1		1		1
1. P =		aha, P =		bhb, P =		chc.
	2		2		2

	1		1		1
2. P =		absinγ, P =		acsinβ, P =		bcsinα.
	2		2		2

	1
3. P = √p(p − a)(p − b)(p − c) , gdzie: p =		(a + b + c), to jest wzór Herona.
	2

4. P = pr, gdzie r − długość promienia okręgu wpisanego w trójkąt.

	abc
5. P =		, gdzie R − długość promienia okręgu opisanego na trójkącie.
	4R

6. P = 2R²sinα sinβ sinγ.