zadanie na udowodnienie
kobe: .Na bokach AB, BC i CA trójkąta ABC zbudowano 3 trójkąty równoboczne:APB, BRC, CQA. Trójkąt BRC
leży po tej samej stronie boku AC co trójkąt ABC. Pozostałe 2 leżą na zewn trójkąta ABC.
Udowodnij że punkty P, R i Q są wpółliniowe, lub są wierzchołkami równoległoboku.
23 mar 20:23
irena_1:
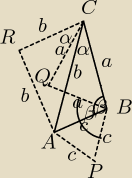
Trójkąty ABC i QRC są przystające (bkb), czyli |RQ|=c
Trójkąty ABC i BPQ są przystające, czyli |PQ|=b
Czworokąt APQR są wierzchołkami równoległoboku
Jeśli ABC jest równoboczny, to Q pokrywa się z A. Punkty P, Q, R są współliniowe
(kąt PQR=60
0+60
0+60
0=180
0)
23 mar 20:56
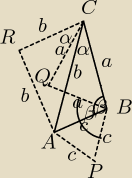 Trójkąty ABC i QRC są przystające (bkb), czyli |RQ|=c
Trójkąty ABC i BPQ są przystające, czyli |PQ|=b
Czworokąt APQR są wierzchołkami równoległoboku
Jeśli ABC jest równoboczny, to Q pokrywa się z A. Punkty P, Q, R są współliniowe
(kąt PQR=600+600+600=1800)
Trójkąty ABC i QRC są przystające (bkb), czyli |RQ|=c
Trójkąty ABC i BPQ są przystające, czyli |PQ|=b
Czworokąt APQR są wierzchołkami równoległoboku
Jeśli ABC jest równoboczny, to Q pokrywa się z A. Punkty P, Q, R są współliniowe
(kąt PQR=600+600+600=1800)