Moneta z dwoma orłami matii: Wśród 65 monet jest jedna z dwoma orłami. Na wybranej losowo monecie wypadł orzeł 6 razy z rzędu. Jaka jest szansa, ze była to moneta z dwoma orłami? Rozwiązanie: Niech A − oznacza zdarzenie 'sześć razy wypadł orzeł', B₁ − rzucano prawidłową monetą, B₂ − rzucano monetą z dwoma orłami. Nie rozumiem, dlaczego:

	1
A/B1 =
	26

A/B₂ = 1 Wyjaśni mi ktoś?

Basia: no jak to dlaczego ? dla A\B₁ masz |Ω| = 2⁶ bo tworzysz ciągi x₁,x₂,x₃,x₄,x₅, x₆ gdzie x_i=O∨R "6 razy O" to jeden ciąg (O,O,O,O,O,O) czyli

	1
P(A/B1) =
	26

dla A/B₂ masz |Ω| = 1⁶ = 1 worzysz ciągi x₁,x₂,x₃,x₄,x₅, x₆ gdzie x_i=O normalnie mówiąc nic innego niż O nie możesz wyrzucić P(A/B₂) = 1

matii: Basia, dziękuję Teraz już jest wszystko jasne

matii: Znów to ja Podoba mi się Twoje rozwiązanie i wydaje się prostsze, i mam pytanie, czy też tak można zrobić:

	1
P(A∩B1) =
	65

	1
P(A∩B2) =
	65

	P(A∩B1)		1   65		1
P(A/B1) =		=		=
	P(B1)		64   65		64

	P(A∩B2)		1   65
P(A/B2) =		=		= 1
	P(B2)		1   65

Czy to jest rozwiązanie błędne?

Mila: Aby dokończyć, trzeba zastosować wzór Bayesa.

	1   *1 65
P((2O)/A)=
	1   64   1   *1+ * 65   65   26

wynik zaskakujący.

matii: Tak wiem, nie napisałem tego, bo mi chodziło tylko o P(A∩B₁) oraz P(A∩B₂) czyli rozumiem, że tak jest dobrze? Jak przeglądam rozwiązania różnych zadań, nie są szczegółowe, nie są podane iloczyny, tylko od razu wzór Bayesa, czy prawdopodobieństwa całkowitego.

Mila: W tym zadaniu dobrze jest narysować drzewko. Po kolacji .

Basia: mati Ty chyba liczysz nie to co trzeba (a może ja źle czytam) trzymając się Twoich oznaczeń masz policzyć P(B₂)/A) natomiast

	1		64
P(A∩B1) = P(A/B1)*P(B1) =		*
	26		65

	1
P(A∩B2) = P(A/B2)*P(B2) = 1*
	65

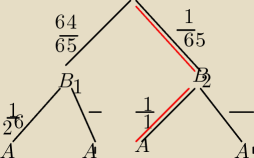
Mila: Doświadczenie ma 2 etapy. B₁ wylosowano monetę prawidłową B₁ wylosowano monetę z 2 orłami A wyrzucono w 6 rzutach 6 orłow pod rząd

	64		1		1		2
P(A)=		*		+		*1=
	65		64		65		65

	P(A∩B2)		1   65		1
P(B2/A)=		=		=
	p(A)		2   65		2

matii: Dobrze przeczytałaś i dziękuję Ci bardzo, że to napisałaś, bo dalej bym źle myślał.

	|A∩B1|
Myślałem, że tak: P(A∩B1) =		, bo ten wzór istnieje.
	|Ω|

matii: Mila, dziękuję za narysowanie drzewka, ułatwi mi to zrozumieć zadanie