Parabola i okrąg Patka: Parabola przecina oś Ox w punktach (0,2) i (0,6) , a jej wierzchołek leży na okręgu (x−4)² + (y−1)²=25− wykonaj rysunek.. Oblicz pozostałe punkty wspólne paraboli i okręgu.

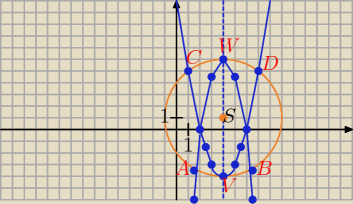
Bogdan: Środek okręgu S = (4, 1), długość promienia okręgu R = 5, miejsca zerowe paraboli: x₁ = 2, x₂ = 6,

	2 + 6
odcięta wierzchołka paraboli xw = xV =		= 4,
	2

rzędna wierzchołka paraboli: (4 − 4)² + (y − 1)² = 25 ⇒ y − 1 = 5 lub y − 1 = −5, stąd y_W = 6, y_V = −4 Przypadek I: Korzystamy z postaci iloczynowej paraboli.

	−3
Parabola z punktem W(4, 6): 6 = a(4 − 2)(4 − 6) ⇒ −4a = 6 ⇒ a =
	2

	−3		−3
y =		(x − 2)(x − 6) ⇒ y =		x2 + 12x − 18
	2		2

Przypadek II: Korzystamy z postaci iloczynowej paraboli. Parabola z punktem V(4, −4): −4 = a(4 − 2)(4 − 6) ⇒ −4a = −4 ⇒ a = 1 y = (x − 2)(x − 6) ⇒ y = x² − 8x + 12 Czy wiesz, co dalej trzeba robić?

AROB: Ale te punkty przecięcia z osią OX (w treści zadania) , to przecież nie takie, tylko (2,0) i (6,0).

Bogdan: Myślę, że powinno być: (2, 0), (6, 0), bo mają to być punkty przecięcia osi x. Ponadto obecnie w szkole ponadgimnazjalnej omawia się wyłącznie parabolę z osią symetrii równoległą do osi y, nie ma w programie nauczania paraboli z osią symetrii równoległa do osi x. Przyjąłem, że Patka popełniła tzw. czeski błąd i przestawiła liczby.

Patka: hmm nie popełniłam błędu, gdyż taka jest treść zadania. A owe zadanie jest z liceum . Też mnie to zadziwiło i skłoniło do wystawienia tego zadania na forum, bo nie mogłam wykonać nawet rysunku.

Bogdan: Owszem, popełniłaś błąd. Należało samemu poprawić treść zadania, jeżeli coś się w nim nie zgadzało, a nie bezmyślnie przepisywać. Punkty, które podałaś: (0, 2), (0, 6) leżą przecież na osi y, a nie na osi x. Powinnaś tu podać: punkty na osi x: (2, 0), (6, 0).

Patka: no to powinnam wyznaczyć wspólne punkty okręgu z parabolą ale nie wiem jak .

Bogdan: Dla znalezienia wspólnych punktów dwóch linii, których równania są znane, trzeba rozwiązać układ tych równań. W tym zadaniu mamy 2 przypadki, a więc trzeba rozwiązać 2 układy równań. Przypadek I: (x − 4)² + (y − 1)² = 25

	3
y = −		x2 + 12x − 18
	2

Tu jedno rozwiązanie już znamy, to punkt W = (4, 6). Przypadek II: (x − 4)² + (y − 1)² = 25 y = x² − 8x + 12 Tu jedno rozwiązanie już znamy, to punkt V = (4, −4). Rozwiąż sama te układy równań.

Patka: Próbowałam je rozwiązać: i jak obliczam wspólny punkt paraboli y= x² − 8x + 12to: (x − 4)² + (y − 1)² = 25 x² −8x+ 16+ y²− 2y +1−25=0 x² −8x+y²−2y−8=0 \teraz za y mam podłożyć parabole? x²−8x+(x²−8x+12)²− 2(x²−8x+12)−8=0 x² − 8x+x⁴+64²+144−2x²+16x−24−8=0 i wychodzi mi x⁴ +63x² + 8 x+112=0 i nie wiem co dalej, to w ogóle dobrze jest? Nie wiem jak ponieś (x²−8x+12)² to wyrażenie do potęgi