dziwolongi wychodzą Kipic: rozwiaz nierownosc lx−lx−3ll<4 wiec na poczatku robilem tak : x≥0 i x<0 x−lx−3l<4 −x+lx−3l<4 x≥3 x<3 x≥3 x<3 i jak tak licze to mi zła odpowiedz wychodzi

Saizou : lx−lx−3ll<4 x−lx−3l<4 i x−lx−3l>−4 dla x≥3 dla x≥3 x−x−3<4 x−x−3>−4 −3<4 (zawsze) −3>−4 (zawsze) dlax x<3 dla x<3 x−(3−x)<4 x−(3−x)>−4 x−3+x<4 x−3+x>−4 2x<7 2x>−1

	7		1
x<		x>−
	2		2

	1
zatem x∊(−		:+∞)
	2

Kipic: a no tak dzięki

akante: czemu pomijasz wartosc bezwzgledna ta pierwzsa tak swobodnie? ja laik

Saizou : nie swobodnie przecież rozpatruję 2 przypadki

Kipic:

	7		1
a jeszcz mam pytanie bo jest x<		i x>−		oraz
	2		2

	1
x≥3 czyli wszytskie R wiec dlaczego sie bierze od −		do +∞ ? ?
	2

Kipic: acha juz wiem

Saizou : zawsze dla iksów z przedziału x∊<3:+∞)

Kipic:

	7
a jednak dalej nie wiem przeciez warunek x<3 jest spelniony przez x<		wiec jak jest ?
	2

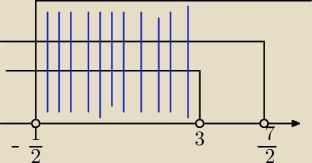
Saizou : zaznaczę tylko

	7		1
x<3 i x<		i x>−
	2		2

Kipic: kurcze dziwnie bo tutaj najp[ierw jst czesc wspolna dla x≥0 i x<0 a poznbiej z dwoch przedzialow suma https://matematykaszkolna.pl/strona/1108.html

Saizou : to można łatwo zapamiętać spójnik i mamy gdy ≤,<, bo odwracamy o 90^o w prawo i otrzymujemy ∧, czyli i spójnik lub mamy gdy ≥,> bo odwracamy o 90^o w prawo i otrzymujemy ⋁ czyli lub

akante: czyli przy mniejszych od zera mamy i a jak jest wiekzse mamy lub?

jikA: Tak jeżeli masz znaleźć argumenty które dają wartości większe to masz lub (oczywiście jeżeli nie ma mnożenia z liczbą ujemną przykład −2|x + 1| ≥ −2 wtedy po uporządkowaniu dostaniemy |x + 1| ≤ 1 czyli spójnik i).