znaleźć równanie prostej Julka28: Znaleźć równanie prostej przechodzącej przez środki cięciw x−y+7=0, 2x−y−1=0 elipsy 64x²+100y²=6400

Mila: 64x²+100y²=6400

	100y2
x2+		=100
	64

x2		y2
	+		=1
102		82

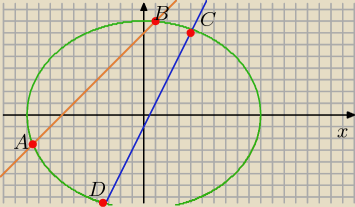
x−y+7=0, 2x−y−1=0 y=x+7 y=2x−1 Znajdź wsp. punktów przecięcia,( podstaw do równania elipsy), środki cięciw, a następnie napisz równanie prostej. rysunek pomoże Ci ustalić.