zadaine
tn: Siatkę ostrosłupa tworzą dwa trójkąty równoboczne o boku a i dwa trójkąty prostokątne. Oblicz
pole powierzchni całkowitej i objętość ostrosłupa.
20 mar 20:17
dero2005:
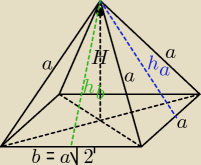
dane: a
| | a√2 | |
hb = √a2 − (b2)2 = √a2 − (a2√2)2 = √a2 − a22 = |
| |
| | 2 | |
| | a2√3 | |
Pb = a*ha + b*hb = |
| + a2 |
| | 2 | |
P
p = a*b = 2a
2
| | √3 | |
Pc = Pp + Pb = a2(3 + |
| ) |
| | 2 | |
20 mar 20:34
tn: a możesz jeszcze narysować tę siatkę ?
20 mar 20:47
dero2005:
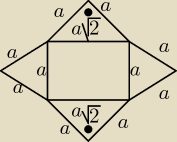
20 mar 20:53
Mila:
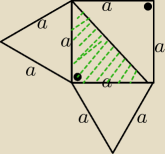
Nalepiej postawić na zielonym trójkącie.
Z P
c nie ma problemu,
P
c=a
2+U{a
2√3{2}
Do V potrzebny nowy rysunek.
Wykonasz?
20 mar 21:00
tn: skąd tutaj prostokąt? Przecież w treści zadania tego nie ma.
20 mar 21:02
tn: @Mila, Twoje rozwiązanie jest OK chyba
zaraz spróbuje kontynuować
20 mar 21:03
tn: Dzięki wielkie Mila

A jak doszłaś do wniosku, że ta siatka będzie właśnie tak wyglądać ?
20 mar 21:09
Mila: Tam jest kwadrat. ( połączenie dwóch trójkątów prostokątnych równoramiennych).
Krawędzie boczne są równe, w takim razie spodek wysokości leży w środku okręgu opisanego na
podstawie ( zielonym Δ), czyli w środku przeciwprostokątnej.
Dalej sam wyciągaj wniosek.
Zrobiłam szybko model.
20 mar 21:21
Mila: Jaki masz wynik?
20 mar 22:07
20 mar 22:47
Mila: 
20 mar 23:19
 dane: a
dane: a

 Nalepiej postawić na zielonym trójkącie.
Z Pc nie ma problemu,
Pc=a2+U{a2√3{2}
Do V potrzebny nowy rysunek.
Wykonasz?
Nalepiej postawić na zielonym trójkącie.
Z Pc nie ma problemu,
Pc=a2+U{a2√3{2}
Do V potrzebny nowy rysunek.
Wykonasz?
 A jak doszłaś do wniosku, że ta siatka będzie właśnie tak wyglądać ?
A jak doszłaś do wniosku, że ta siatka będzie właśnie tak wyglądać ?
