Dowód- środkowe w trójkącie
Alek: Wykaż, że w dowolnym trójkącie ABC prawdziwa jest podwójna nierówność
| 3(a+b+c) | |
| < Sa + Sb + Sc < a+b+c, gdzie a, b, c oznaczają długości odpowiednich |
| 4 | |
boków trójkąta, S
a, S
b, S
c − długości środkowych poprowadzonych odpowiednio do boków
o długościach a, b, c.
20 mar 20:04
ICSP: a wzór na długość środkowej jest ci znany ?
20 mar 20:16
Alek: jest mi znany, ale nie poznawaliśmy go na lekcji i nie wiem czy da się zrobić to jakoś z
ominięciem tego wzoru.
20 mar 20:20
ICSP: ale po co sobie utrudniać życie ?
Zrobienie z ominięciem wzoru najczęściej polega na wyprowadzeniu wzoru.
20 mar 20:21
Alek: no dobrze, a jak zrobić to z zastosowaniem tego wzoru?
20 mar 20:22
ICSP: najpierw trzeba napisać wzory dla wszystkich trzech środkowych
20 mar 20:23
Alek:
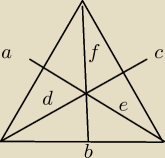
d=1/2
√2a2+2b2−c2
e=1/2
√2b2+2c2−a2
f=1/2
√2a2+2c2−b2
Czy ja dobrze to rozpisałem?
20 mar 20:32
ICSP: rozpisałeś dobrze ale niestety nic to nie da

Ja bym stawiał na rozwiązanie geometryczne. Daj mi 10 min to napiszę całość
20 mar 20:47
Alek: ok, z góry dzięki

20 mar 20:51
ICSP:
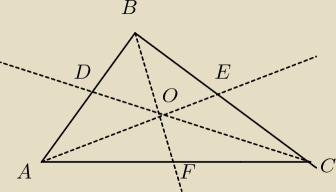
u mnie : |AB| = a , |BC| = b , |AC| = c i odpowiednio |BF| = S
c , |DC| = S
a , |AE| = S
b
i mam :
|BO| + |AO| > |AB| − dla trójkąta ABO
|AO| + |CO| > |AC| − dla trójkąta ACO
|BO| + |CO| > |BC| − dla trójkąta BCO
2(|BO| + |AO| + |CO|) > a + b + c
| 4 | |
| (|BF| + |AE| + |CD|) > a + b + c |
| 3 | |
| 3 | |
| (a + b + c) < Sa + Sb + Sc |
| 4 | |
co dowodzi lewej nierówności. Teraz trzeba dowieść prawą :
|EF| + |EB| > |BF|
|ED| + |DA| > |AE|
|DF| + |FC| > |CD|
dodając stronami dostaniesz że
| | 1 | |
a + b + c > Sa + Sb + Sc (ponieważ z twierdzenia Talesa |EF| = |
| |AB| itd) |
| | 2 | |
20 mar 21:01
Alek: Dzięki wielkie

20 mar 21:30
as: | | 1 | |
skad wiemy, ze IEFI= |
| IABI ? |
| | 2 | |
26 maj 19:49
Eta:
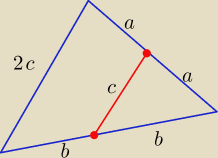
26 maj 20:04
 d=1/2 √2a2+2b2−c2
e=1/2 √2b2+2c2−a2
f=1/2 √2a2+2c2−b2
Czy ja dobrze to rozpisałem?
d=1/2 √2a2+2b2−c2
e=1/2 √2b2+2c2−a2
f=1/2 √2a2+2c2−b2
Czy ja dobrze to rozpisałem?
 Ja bym stawiał na rozwiązanie geometryczne. Daj mi 10 min to napiszę całość
Ja bym stawiał na rozwiązanie geometryczne. Daj mi 10 min to napiszę całość

 u mnie : |AB| = a , |BC| = b , |AC| = c i odpowiednio |BF| = Sc , |DC| = Sa , |AE| = Sb
i mam :
|BO| + |AO| > |AB| − dla trójkąta ABO
|AO| + |CO| > |AC| − dla trójkąta ACO
|BO| + |CO| > |BC| − dla trójkąta BCO
2(|BO| + |AO| + |CO|) > a + b + c
u mnie : |AB| = a , |BC| = b , |AC| = c i odpowiednio |BF| = Sc , |DC| = Sa , |AE| = Sb
i mam :
|BO| + |AO| > |AB| − dla trójkąta ABO
|AO| + |CO| > |AC| − dla trójkąta ACO
|BO| + |CO| > |BC| − dla trójkąta BCO
2(|BO| + |AO| + |CO|) > a + b + c

