geometria analityczna andrzej: Mam problem zzadniem, nie wiem po prostu czemu tak nie mozna liczyc: Dany jest okrag o rownaniou x² + 6x + y² −2y = −9 i prosta y=mx +2 Wyznacz zbior wszystkich wartosci m dla ktorych prosta i okrag maja dokladnie 2 punkty wspolne: i teraz robie tak ze tam gdzie jest rownanie okregu podstawiam moja prosta i mam x²(1+m²) + x(6+2m) + 9 = 0 no i teraz stawiam warunki : a≠0 Δ>0

	√3		√3
wychodzi mi tam m∊(−		,		)
	2		2

a w ksiazce jest calkiem inna metoda robione i calkiem inny wyniki to co robie zle i czemu tak nie mozna?

Mila: Masz błąd rachunkowy, ma być +5 a nie +9. Jaki wynik ma być?

andrzej:

	3
ahaaaaa bo nie przenioslem 9 i <= r2 ? (0,		)
	4

andrzej: no ale jak 4 sie skracaja

Mila: Czy już zrobiłeś, czy pomagać?Słusznie,jest dobrze. Wychodzi dobrze Twoim sposobem.

andrzej: pomoz bo nie wiem co robie zle pewnie maly blad a duzo znaczy

andrzej: jaaaaa wuem juz wiem jaki glupi co ja wgl zrobilem bylo 24 m − 32m²<0 a ja niestety strasznie pisze, i zamiast 24 m to mialem samo 24 dzieki

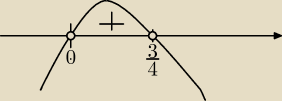
Mila: m²+1>0 dla m∊R i Δ>0 Δ=(6+2m)²−4*9(m²+1)=36+24m+4m²−36m²−36 Δ=24m−32m² 24m−32m²>0 /:8 3m−4m²>0 m(3−4m)>0

	3
m=0 lub m=		parabola skierowana w dół
	4

	3
m∊(0,		)
	4