zad elo: PROSZE O POMOC, JA STARAM SIĘ POMAGAĆ POD RÓŻNYMI NICKAMI,dzis jako "elo", A POMOCY NIE OTRZYMAŁAM... ***mat*** w trapezie ABCD dwusieczna poprowadzona z wierzchołka B dzieli bok CD w punkcie E, tak, że EB II AD, oblicz miary kątów tego trapezu, przy czym (α=I<AI, β=I<BI, γ−kąt przy wierzchołku c i δ analogicznie kąt przy wierzchołku D)

tim: Nie ma nic więcej?

elo: żadnych danych więcej nie podali, ale jak chcesz to mam jeszcze jedno zadanie którego nie umiem. oba są na poziomie trzeciej liceum klasa maturalna profil z rozszerzona matematyką, zadanie na rozgrzewkę z okazji pierwszej lekcji matmy po wakacjach

tim: Mi nie wychodzi nic. Może Bogdan coś wymyśli

tim: Wyszło mi, że są kąty β, 180−0,5β, 0,5β i 180−β. Tyle. Zależnie od β będą różne kąty. Bogdan coś może wymyśli.

elo: a tu chyba da sie wyliczyć wartość kątów... dokładną i nie zależną od żadnego z nich.. jak myślisz Bogdanie?

tim: Dajmy mu moment

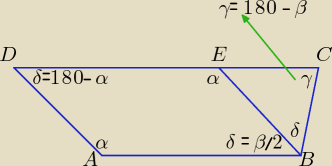
Bogdan: ABED jest równoległobokiem. Można wyznaczyć miary kątów wewnętrznych trapezu ABCD w zależności od miary jednego z kątów wewnętrznych tego trapezu.

tim: Czyli miałem racje Yeah...

Bogdan: Trzeba przyjąć miarę jednego z kątów trapezu za wiadomą, np.: α, wtedy: β = 2δ = 2*(180^o − α) = 360^o − 2α γ = 180^o − β = 180^o − (360^o − 2α) = 2α − 180^o δ = 180^o − α

Bogdan: Jeśli przyjmiemy za wiadomą miarę β, to:

	1
α = 180o − δ = 180o −		β
	2

γ = 180^o − β

	1
δ =		β
	2