stereometria Anka: Podstawą ostrosłupa jest prostokąt o bokach 4 i 4√2. Wszystkie krawędzie boczne ostrosłupa mają dł. 4. Oblicz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

	5√3		√21
Obliczyłam, wyszło −		a ma wyjść −		. I nie wiem gdzie jest bład...
	12		21

Anka: Haaaalo. Pomóżcie

Anka: Ludzieee. Łatwe zadanie

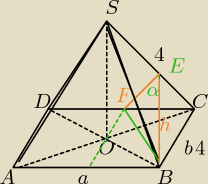
Mila: ΔBCS− Δrównoboczny o boku 4.

	4√3
h=		=2√3
	2

ΔDCS− Δrównoramienny prostokątny: a²=4²+4²=32 a=4√2 Punkt E leży w połowie boku CS, FE||SD i równe połowie SD FE=2 FB²=4²+(2√2)² FB²=16+8=24 24=(2√3)²+2²−2*2*2√3 cosα

	−√3
cosα=
	3

Mila: Aniu, to dla uczniów nie jest łatwe zadanie, zwykle nie zauważają , że dwie ściany są Δprostokątnymi.

Anka: Mila, a skąd wiadomo, że te 2 ściany to trójkąty prostokątne? Ten wynik, który otrzymalas tez nie jest prawidłowy

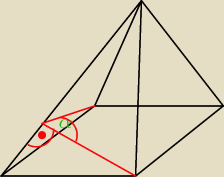
Anka: i mi się wydaje że ten kąt powinien być tak zaznaczony

Anka: i co z tym

Mila: Dwie ściany są trójkątami równobocznymi o boku 4. Dwie ściany są trójkątami o bokach:4√2,4,4 z tresci zadania (4√2)²=4²+4² 16*2=16 + 16 32=32 na podstawie tw. odwrotnego do tw. Pitagorasa ten Δ jest trójkatem prostokątnym. ( napisałam to w 4 linijce poprzedniego wpisu). W takim razie Twój kąt jest błędnie zaznaczony. Może inne dane są w zadaniu?