Dwie kule bez zwracania matii: Mamy w urnie n kul, przy czym n może być równe 2, 3, 4, 5 z jednakowym prawdopodobieństwem. Kule są ponumerowane liczbami od 1 do n. Losujemy kolejno dwie kule bez zwracania i zapisujemy cyfry z tych kul w kolejności wylosowania. Zapisana liczba okazała się być mniejsza od 44. Jakie jest prawdopodobieństwo, że n było równe 3?

	4
Prawidłowa odpowiedź to
	15

matii: uuu ale strasznie poszło w dół

matii: nikt mi nie pomoże?

Mila: A −zapisana liczba mniejsza od 44

	1		1		1		1		15		3		3		15
P(A)=		*1+		*1+		*1+		*		=		+		=
	4		4		4		4		20		4		16		16

dla n=2 lub 3 lub 4 wszystkie liczby dwucyfrowe sa mniejsze od 44 dla n=5 15 liczb mniejszych od 44 5 większych od 44 są to {45,51,52,53,54}

	P(A∩N3)		1		15		1		16		4
P(A/N3) =		=		:		=		*		=
	P(A)		4		16		4		15		15

matii: Kochana jesteś. Dziękuję za pomoc

Mila:

matii: Witam, znów to ja. Prosiłbym o wyjaśnienie P(A∩N₃). −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Wiemy, że N₃ = (12, 21, 13, 31, 23, 32) A = (12, 21, 13, 31, 23, 32, 14, 41, 24, 42, 34, 43, 15, 25, 35) Ω = 20 A∩N₃ = (12, 21, 13, 31, 23, 32) = 6

	A∩N3		6		3		1
P(A∩N3) =		=		=		, a powinno być		.
	Ω		20		10		4

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Co ja źle rozumiem? Prosiłbym o wyjaśnienie

matii: Mila, wyjaśnisz mi?

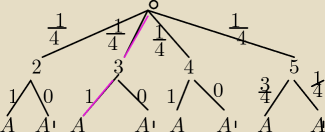
Mila: P(A∩N₃) liczysz z różowej ścieżki. Stosujesz wzór Bayesa.

Mila: Jaki dział przerabiasz?

matii: Przerabiamy dział prawdopodobieństwa całkowitego oraz wzór Bayesa, więc bez obaw znam te wzory Dziękuję za narysowanie drzewka, jednak już rozumiem. Aby być pewnym, czy możesz sprawdzić, że:

	2
przy n=2: P(N2) =		= 1
	2

	6
przy n=3: P(N3) =		= 1
	6

	12
przy n=4: P(N4) =		= 1
	12

	3
przy n=5: P(N5) =
	4

Dobrze?

Mila: Jeśli chodzi o dolne piętro drzewka to tak, popatrz na formalne zapisy, na pewno masz w zeszycie.

matii: Tak, chodziło mi o dolne drzewko. Dziękuję za sprawdzenie