monotoniczność kosmita: Witam Jest ktoś w stanie mi pomóc z tym przykładem ? Jest funkcja i mam określić jej monotoniczność na przykładzie wzoru. Więc tak : f(x)=4−x² X∊R_ x1>x2⇒x1²<x2²⇒ −x1²>−x2²⇒ −x1²+4>−x2²+4⇒ f(x1)>f(x2) I odpowiedź to funkcja jest rosnaca w R ujemnych A teraz mam pytanie jak wyglądałaby ta funkcja gdyby była określona przedziałem (−∞,2) Baardzo proszę o pomoc Pozdrawiam.

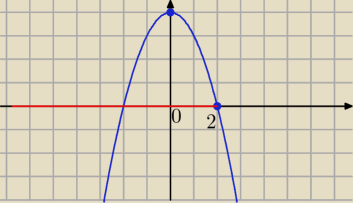
Eta: f(x) ↗ dla x€(−∞,0) f(x) ↘ dla x€ (0,2)

kosmita: Kurcze a można by to było zapisać w postaci nie graficznej ? Tak jak ja podałem wcześniej ? Byłbym wdzięczny gdyż z tego mam właśnie zadania.

kosmita: Pomoże ktoś ?

krystek: x₁<x₂ i x₁,x₂∊R₊ Badasz różnicę f(x₁)−f(x₂)=(4−x₁²)−(4−x₂²)=x₂²−x₁²=(x₂−x₁)(x₂+x₁)>0 ⇒ f(x₁)−f(x₂)>0 ⇒f(x₁)>f(x₂) stad f jest malejaca

kosmita: ale to jest dla funkcji określonej przedziałem (−∞,2) ?

krystek: a skąd wziąłeś ten przedział?

krystek: wtedy badasz dla x∊(−∞,0 i (0 ,2)

kosmita: no to ok tylko problem jest taki ,że ja nie potrafię tego zapisać...Nie wiem czy ja mam gdzieś podstawiać sobie potem te liczby z przedziału czy jak ?

krystek: Eta Tobie graficznie pokazała gdzie f rośnie a gdzie maleje Ty masz zbadać , więc z definicji f↗⇔dla x₁,x₂∊D gdy x₁<x₂⇒F(x₁)<f(x₂)⇒f(x₁)−f(x₂)<0 (analogicznie malejąca tylko f(x₁)>f(x₂) )

kosmita: No dobra a jaka będzie ta funkcja ? −x²+6x w(−∞,3)

kosmita: Też mam robić dla dwóch przedziałów ? w sensie od (−∞,0) i tu wybieram liczby ujemne i od (0,3) ? Ttutaj w tym drugim przedziale zero ma być domknięte czy otwarte ?

kosmita: Kto mi pomoże ?