Problem ze wzorem funkcji liniowej Matek: Czesc. Mam maly problem z funkcja liniowa. Ma ona wzor : y jest rowne wartosc bezwzgledna z x podzielic przez x. Na podstawie tego wzoru mam wyznaczyc punkty przeciecia z osia x i y, ale kompletnie nie wiem, jak zabrac sie za to zadanie. Czy ktos moze pomoc? Dziekuje

tim:

	|x|
f(x) =		?
	x

Matek: dokładnie tak

tim: Więc tak. Spróbuj określić dziedzinę.

Matek: x należy do zbioru liczb rzeczywistych

tim: Nie...

Matek: Chodzi Ci o to, jakie wartości są przypisane argumentom?

tim: Jakie wartości NIE MOGĄ być przypisane argumentom...

Matek: Wiem, że wychodzę na ciemniaka, ale dziś miałe pierwszą lekcję z funkcji liniowych. Chodzę do klasy o profilu humanistycznym. Matematyki uczy mnie 80 letni dziadek i niestety nie potrafi tłumaczyć, nie mówiąc już o uczeniu. Czy mógłbyś podsunąć mi pomysł na rozwiązanie tego zadania? W gimnazjum latałem na trójach i czwórach, a teraz mam spory problem z matematyką, bo mój nauczyciel nie uczy

tim: Poczytaj: https://matematykaszkolna.pl/strona/22.html

Matek: Miałem podobny przykład: y jest równe wartości bezwzględnej z x. Narysowałem układ, w którym prosta przechodziła przez punkty (1,1) , (2,2) itd. Była to wartość bezwzględna, dlatego trzeba było tę prostą odbić względem osi x. Nie jestem pewny, ale w wypadku wzoru, o który się rozchodzi prawdopodobnie trzeba wykonać symetrię względem osi y. Tylko nie jestem tego pewny...

Matek: Aha. Przykłady, które dał profesorek nie wymagały wyznaczanie dziedziny. Chodziło tylko o punkt przecięca z osią x i y i o narysowanie funkcji w układzie współżędnych

tim: Dla y = |x| wykres wygląda jak V. Ale nie można odczytywać takich rzeczy z wykresu. Powiem tak. Funkcja f(x) przecina oś Ox, dla y = 0, a oś Oy dla x = 0. Zatem podstawiasz:" y = |x| 0 = |x| x = 0 y = |x| y = |0| y = 0 Zatem punkty przecięcia to (0,0) (0,0) (jest to jeden ten sam punkt). To samo w tym przykładzie. Jednakże należy uwzględnić dziedzinę. Odpowiedz mi: przez jakie liczby nie można dzielić (nie mogą być w mianowniku)...

Matek: Oczywiście 0

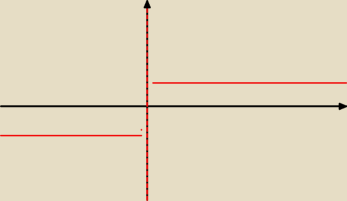
tim: No więc wszystko (tabelkę, wykres) robisz bez 0. Zatem dziedzina: Df: R \ {0} (rzeczywiste bez 0) Zatem spróbuj zrobić tabelkę dla tej twojej funkcji (bez 0!). Spróbuj coś zauważyć. Jeżeli miałeś wartość bezwzględną spróbuj ją rozpisać i zobacz co powstanie (przed zrobieniem tabelki).

Matek: Dobra. Jaki jest wzór funkcji, którą pokazałeś w układzie?

tim: Najpierw rozwiąż potem ci powiem

Matek: Jako argumenty wybrałem liczby 1,2,3 i 4. Żeby obliczyć wartości, trzeba wyliczać wartości bezwzględne argumentów (y=|x|) ?

tim: Następna uwaga. Najlepiej wziać (jeżeli nie wyklucza dziedzina). Kilka ujemnych i dodatnich, zatem: −2, −1, 1, 2 (są o wiele lepsze). Tak trzeba obliczyć |x| i podzielić przez liczbę x.

Matek: No racja Powiem Ci wprost, jesteś gość. Naprawdel wielkie dzięki.Dobra to jaki będzie wzór tej funkcji?

Matek: a i dlacego w tą całą zabawę z tabelkami nie nie włącza się 0?

tim: Wzór SWOJEJ funkcji jest podany. Wzór MOJEJ powiem jak narysujesz mi wzór swojej ... Dlatego, że przed chwilą wykluczyliśmy 0 (dziedzina), gdyż jak wstawisz 0, wyskoczy ci ERROR

Matek: narysowałem tą funkcję w układzie, ale nie chce czekac na załadowanie.

	|x|
y=		najprawdopodobniej to jest wzór mojej funkcji chyba że sie myle bo tak tez
	x

moze byc

Matek: Z argumentu trzeba wyliczyć wartość bezwzględną i wynik podzielić przez wartość argumentu

tim: Czyli dla x = 1, y = 1, dla x = 2, y = 1, dla x = 3, y = 1, więc dla x ∊ (0, +∞) y = 1 A dla x ∊ (−∞,0) y = −1. I tak, ja narysowałem wykres twojej funkcji.

Matek: Szczerze Ci powiem, że masz głowę, bo ja nie potrafie myśleć tak logicznie. Jestem pełen podziwu. I oczywiście dziękuję za cierpliwość i pomoc. Cześć