Trójkąt prostokątny w okręgu.
misha: Oblicz długości boków trójkąta prostokątnego, wpisanego w okrąg o promieniu długości r, którego
jedna z przyprostokątnych ma długość a.
19 mar 18:19
dero2005:
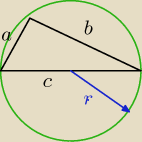
dane:
a, r
c = 2r
b =
√c2 − a2 =
√(2r)2 − a2 =
√4r2 − a2
19 mar 18:39
Mila:
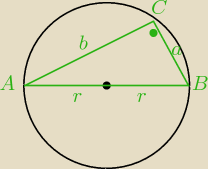
środek okręgu opisanego na Δ prostokątnym leży w środku przeciwprostokątnej
∡C=90
0 jako wpisany oparty na średnicy.
|AB|=2r
(2r)
2=a
2+b
2
4r
2−a
2=b
2
b=
√4r2−a2
19 mar 18:40
misha: Dziękuję!
19 mar 19:41