zadania z geometri lars: proszę o pomoc 1. wykaz ze nie istnieje trapez równo ramienny ABCD o podstawach AB i CD w którym kat ostry ma miarę 30 stopni przekątna Ac o długości 12 tworzy z ramieniem trapezu kat o mierze 120 stopni 2. w trójkącie ABC długość boków maja się do siebie jak 4:5:6 udowodni ze w tym trójkącie cos²α =cos β gdzie αi β to miary kątów wewnętrznych trójkąta ABC 3. dany jest trójkąt ABC w którym BC=6 miara konta CAB jest równa 60stopni a miara kata ABC jest równa 45 oblicz długość boku AB 4.w trójkącie ABC długość boków są równe 2,5 i 6 oblicz wartość sinusów wszystkich kątów wewnętrznych tego trójkąta

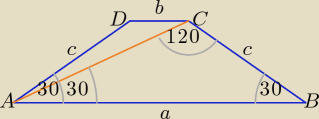
Bogdan: Zad. 1. Rysunek wyjaśnia sprawę.

Eta: W zad2/ powinno być , że cos2α = cosβ

Bogdan: Zad. 2. Skorzystaj z twierdzenia cosinusów i wyznacz cosα oraz cosβ.

Bogdan: Zad. 3. Skorzystaj z twierdzenia sinusów oraz z faktu: sin75^o = sin(45^o + 30^o)

Bogdan: Eto, w zadaniu 2 jest cos²α = cosβ

Bogdan: Zad. 4. Można różnie rozwiązać, np. tak:

	a		b		c
Korzystamy z twierdzenia sinusów:		= 2R,		= 2R,		= 2R.
	sinα		sinβ		sinγ

Mamy dane: a = 2, b = 5, c = 6.

	a*b*c
R =		, gdzie PΔ to pole trójkąta, które można wyznaczyć np. wzorem Herona.
	4PΔ

Eta: OK .... cosα= ³₄ , cosβ= ⁹₁₆ więc cos²α= cosβ