planimetria cromer : prosze o pomoc 1. długość boków trójkąta ABC są kolejnymi liczbami naturalnymi. Miara kata , który leży naprzeciw najdłuższego boku jest dwa razy większy od miary kata o najmniejszej mierze oblicz długości boków trójkąta ABC 2.dany jest równoramienny trójkąt ABC w którym podstawa AB ma długość 8 a długość promienia okręgu wpisanego w ten trójkąt wynosi 2 oblicz iloczyn sinusów wszystkich kątów wewnętrznych tego trójkąta 3. w trójkącie ABC na bokach AB i BC wybrano odpowiednio punkty K i L w taki sposób ze |AB/KB| =√2 , |BC/BL |= 2 √2 Wykaz ze pole trójkąta KBL jest czterokrotnie mniejsze od pola trójkąta ABC 4.w trójkącie ABC są dane długości boków AC=6 i BC= 10 a miara kata ACB wynosi 30stopni w trójkącie KLM są dane długości boków KM=3 √2 LM= 5 √2 oraz cos |kata LMK|=2/3 sprawdź czy trójkąty ABC i KLM są podobne

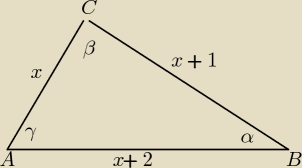
AS: β = 2*α γ = 180^o − 3*α Z tw. sinusów

x + 1		x		x + 2		x
	=				=
sinγ		sinα		sinβ		sinα

(x + 1)*sinα = x*sinγ (x + 2)*sinα = x*sinβ ale sinγ = sin(180^o − 3*α) = sin3α = 3*sinα − 4*sin³α sinβ = sin2α = 2*sinα*cosα Podstawiam do ostatniego związku (x + 1)*sinα = x*(3*sinα − 4*sin³α) | :sinα ≠ 0 (I) (x + 2)*sinα = x*2*sinα*cosα | :sinα ≠ 0 (II) I x + 1 = x*(3 − 4*sin²α) x + 1 = 3*x − 4*x*sin²α 1 = 2*x − 4*x*(1 − cos²α) 1 = 2*x − 4*x+ 4*x*cos²α 1 = 4*x*cos²α − 2*x 1 = 2*x*(2*cos²α − 1) II

	2
x + 2 = 2*x*cosα ⇒ 2 = 2*x*cosα − x = x*(2*cosα − 1) ⇒ 2 =
	2*cosα − 1

Podstawiam x z II do I

	2
1 = 2*		*(2*cos2α −1 )
	2*cosα − 1

2*cosα − 1 = 8*cos²α − 4 po uporządkowaniu 8*cos²α − 2*cosα − 3 = 0 Po wyliczeniu Δ otrzymamy dwa rozwiązania cosα = −0.5 ⇒ α = 120^o odpada cosα = 0.75 ⇒ α = 41^o 25' Szukany bok;

	2		2		2
x =		=		=		= 4
	2*cosα − 1		2*0.75 −1		0.5

Szukane boki: 4 , 5 , 6

AS: Korekta w II

	2
x + 2 = 2*x*cosα ⇒ 2 = 2*x*cosα − x = x*(2*cosα − 1) ⇒ x =
	2*cosα − 1

Eta: Można też tak: Ja użyję właściwych dla liczb naturalnych oznaczeń długości boków : n , n+1, n+2 dla n€N+ kąt leżący naprzeciw boku "n+2" −−− oznaczam : 2α " " " "n" −−−− " " : α podobnie ze wzoru sinusów:

n+2		n
	=		to ( n+2)*sinα= n *2 sinα*cosα / : sinα
sin2α		sinα

	n+2
mamy: cosα=
	2n

Teraz ze wzoru cosinusów :

	n+2
n2 = ( n+2)2 + ( n+1)2 −2*( n+2)*( n+1) *
	2n

po wykonaniu działań i redukcji otrzymamy: n² −3n −4=0 Δ= 25 √Δ=5 to: n₁ = 4 n₂= −1 −−− odrzucamy bo n€N+ n = 4 n+1 = 5 n+2 = 6 odp: 4 , 5 , 6 są długościami boków tego trójkąta

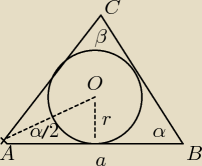
AS: Zadanie 2 Sposób 1 tg(α/2) = r/(a/2) = 2/4 = 0.5 ⇒ α = 53^o08' β = 180^o − 2*α = 180^o − 2*53^o08' = 73^o 44' sin(α)*sin(α)*sin(β) = 0.8*0.8*0.96 = 0.6144 Sposób 2

	2*tg(α/2)		2*0.5		1		4
tg(α/2) = 0.5 , tg(α) =		=		=		=
	1 − tg2(α/2)		1−0,52		0.75		3

	tg(α)		4/3		4/3		4
sin(α) =		=		=		=
	√1 + tg2(α)		√1 + (4/3)2		5/3		5

sin(β) = sin(180^o − 2*α) = sin(2*α) = 2*sin(α)*cos(α) = 2*sin(α)*√1 − sin²(α)

	4		4		3		24
sin(β) = 2*		*√1 − (4/5)2 = 2*		*		=
	5		5		5		25

	4		4		24		384
sin(α)*sin(α)*sin(β) =		*		*		=		= 0.6144
	5		5		25		625

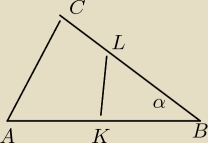
AS: Zadanie 3

	AB
Dane:		= √2 ⇒ AB = √2*KB
	KB

	BC
		= 2√2 ⇒ BC = 2*√2*BL
	BL

	1
PΔBKL =		*KB*BL*sin(α)
	2

	1		1		1
PΔABC =		*AB*BC*sin(α) =		*√2*KB*2*√2*BC*sin(α) =		*4*KB*BL*sin(α)
	2		2		2

Stąd wniosek PΔABC = 4*PΔBKL

AS: Zadanie 4 Dwa trójkąty są podobne jeżeli dwa boki są odpowiednio proporcjonalne a kąty między nimi zawarte są równe.

KM		3*√2		√2
	=		=
AC		6		2

ML		5*√2		√2
	=		=
BC		10		2

Wiemy już,że boki są proporcjonalne

	√5
cos(β) = 2/3 ⇒ sin(β) = √1 − cos2(β) = √1 − 4/9 =
	3

Wartość uzyskana jest różna od 1/2 = sin(30^o) Wniosek: trójkąty te nie są podobne.

AS: Korekta do zadania 3

	1		1		1
PΔABC =		*AB*BC*sin(α) =		*√2*KB*2*√2*BL*sin(α) =		*4*KB*BL*sin(α)
	2		2		2