 np tak ...
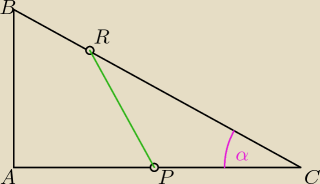
policz α a potem z twierdzenia cosinusów
np tak ...
policz α a potem z twierdzenia cosinusów
| I AB I | 5 | |||
sin α = | = | |||
| I BC I | 13 |
| IAC I | 12 | |||
cos α = | = | |||
| I BC I | 13 |
| h | 5 | ||
= sin α = | |||
| 6 | 13 |
| 5 | 30 | |||
h = 6* | = | |||
| 13 | 13 |
| y | 12 | ||
= cos α = | |||
| 6 | 13 |
| 12 | 72 | |||
y = I CQ I = 6* | = | |||
| 13 | 13 |
| 72 | 130 | 72 | 58 | |||||
I RQ I = I CR I − y = 10 − | = | − | = | |||||
| 13 | 13 | 13 | 13 |
| 58 | ||
z = I RQ I = | ||
| 13 |
| 30 | 58 | 900 | 3364 | |||||
x2 = h2 + z2 = ( | )2 + ( | )2 = | + | = | ||||
| 13 | 13 | 169 | 169 |
| 4 264 | ||
= | ||
| 169 |
| √ 4 264 | 2 √1066 | |||
x = | = | |||
| 13 | 13 |
| 2 √1 066 | ||
Odp. I PR I = x = | ≈ 5,02 | |
| 13 |