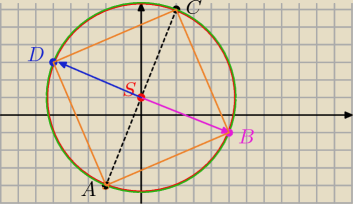
 AC − przekątna kwadratu:
Punkty A=(−2,−4) i C=(2,6) są wierzchołkami kwadratu ABCD.
środek AC:
S=(xs; ys)=(0,1)
|AC|=√42+102=√116=√4*29=2√29
SC→=[2,5] wektor SC→jest prostopadły do wektora SB→
SB→[5,−2]
S=(0,1)→translacja o wektor [5,−2]⇒B=(0+5,1−2)=(5,−1)
S=(0,1)→translacja o wektor [−5,+2]⇒D=(0−5,1+2)=(5,3)
R=√29
b) Równanie okręgu opisanego na kwadracie
x2+(y−1)2=29
AC − przekątna kwadratu:
Punkty A=(−2,−4) i C=(2,6) są wierzchołkami kwadratu ABCD.
środek AC:
S=(xs; ys)=(0,1)
|AC|=√42+102=√116=√4*29=2√29
SC→=[2,5] wektor SC→jest prostopadły do wektora SB→
SB→[5,−2]
S=(0,1)→translacja o wektor [5,−2]⇒B=(0+5,1−2)=(5,−1)
S=(0,1)→translacja o wektor [−5,+2]⇒D=(0−5,1+2)=(5,3)
R=√29
b) Równanie okręgu opisanego na kwadracie
x2+(y−1)2=29
| 1 | 1 | |||
c) P□= | |AC|2= | *116=58 | ||
| 2 | 2 |
| xA+xB | yA+yB | 1 | ||||
S( | , | ) , R= | |AC|=.... | |||
| 2 | 2 | 2 |
| d2 | ||
P(kwadratu)= | = 2R2=... d= 2R−− długość przekątnej kwadratu | |
| 2 |

