POMOCY kika22c: 1. Dane są macierze A [4 1 5] B [3 2 0] [2 3 0] [2 3 5] [1 2 1] [1 −1 2] a) Oblicz iloczyn macierzy B*A b) Wyznacz macierz odwrotną do macierzy A 2. Rozwiąż układ metodą akademicką a) {2x + 3y +z = 8 {3x + y – 2z = 5 { x + 3y –z =−2 b) {2x – 3y + 5z = 1 {3x – 5y – 10z = −4 3. Oblicz pole trójkąta ABC o wierzchołkach A(−2, −3) B (2, 1) C ( −1, 5) 4. Oblicz iloczyn skalarny wektorów u i v oraz cos konta jaki one tworzą u = ( −3, 5, 4) v = (2, 3, 1) 5. Napisz równanie ogólne parametryczne i kierunkowe płaszczyzny przechodzącej przez punkt P (2, 3, −6) prostopadłej do płaszczyzn π₁ x + y + z −5 = 0 π₂ x – y + 2 = 0 6. Przedstaw prost w postaci kanonicznej 3x – y – z + 2 = 0 x – y + z + 3 = 0 JEŚLI KTOŚ MOŻE POMÓC TO BARDZO PROSZĘ. ZALEŻAŁO BY MI NA ROZWIĄZANIACH OD DESKI DO DESKI

b.: znaczy mamy za Ciebie rozwiązać zadanie domowe? bo jeśli chcesz coś zrozumieć, to rozwiązania od deski do deski nie mają sensu... iloczyn macierzy to łatwa rzecz, tylko trzeba wiedzieć, jak to się robi; zajrzyj do podręcznika (lub np. wikipedii), a dalej raczej sobie poradzisz −− napisz co Ci wyszło, sprawdzimy...

kika22c: Nie zadanie domowe tylko ważny test który chciałabym mieć rozwiązany by móc rozwiązywać zadania o podobnej treści. a że matma to mój słaby punkt liczę na na kogoś kto pomoże!

evil_woodworm: zad3: Obliczam współrzedne wektorów |AB| i |BC| |AB|=[x_b−x_a; y_b−y_a]=[2−(−2); 1−3]=[4; −2] |BC|=[x_c−x_b; y_c−y_b]=[−1−2; 5−1]=[−3;4]

	4*4−(−3)*(−2)		16−6		10
P△=		=		=		=5[j2]
	2		2		2

Odp.P△=5j²

evil_woodworm: zad2: Jeżeli metoda akademicka to metoda wyznaczników, to: a) {2x + 3y +z = 8 {3x + y – 2z = 5 { x + 3y –z =−2 [ 8 3 1] W= [ 5 1 −2] =−2+9−6−1+12+9=21 [−2 3 −1] [ 8 3 1] W_x= [ 5 1 −2] =−8+15+12+2+15+48=84 [−2 3 −1] [2 8 1] W_y= [3 5 −2] =−10−6−16−5+24−8=−21 [1 −2 −1] [2 3 8] W_z= [3 1 5] =−4+72+15−8+18−30=63 [1 3 −2]

	Wx		84
x=		=		=4
	W		21

	Wy		−21
y=		=		=−1
	W		21

	Wz		63
z=		=		=3
	W		21

evil_woodworm: zad2: Jeżeli metoda akademicka to metoda wyznaczników, to: a) {2x + 3y +z = 8 {3x + y – 2z = 5 { x + 3y –z =−2 [ 8 3 1] W= [ 5 1 −2] =−2+9−6−1+12+9=21 [−2 3 −1] [ 8 3 1] W_x= [ 5 1 −2] =−8+15+12+2+15+48=84 [−2 3 −1] [2 8 1] W_y= [3 5 −2] =−10−6−16−5+24−8=−21 [1 −2 −1] [2 3 8] W_z= [3 1 5] =−4+72+15−8+18−30=63 [1 3 −2]

	Wx		84
x=		=		=4
	W		21

	Wy		−21
y=		=		=−1
	W		21

	Wz		63
z=		=		=3
	W		21

evil_woodworm: zad2: Jeżeli metoda akademicka to metoda wyznaczników, to: a) {2x + 3y +z = 8 {3x + y – 2z = 5 { x + 3y –z =−2 [ 8 3 1] W= [ 5 1 −2] =−2+9−6−1+12+9=21 [−2 3 −1] [ 8 3 1] W_x= [ 5 1 −2] =−8+15+12+2+15+48=84 [−2 3 −1] [2 8 1] W_y= [3 5 −2] =−10−6−16−5+24−8=−21 [1 −2 −1] [2 3 8] W_z= [3 1 5] =−4+72+15−8+18−30=63 [1 3 −2]

	Wx		84
x=		=		=4
	W		21

	Wy		−21
y=		=		=−1
	W		21

	Wz		63
z=		=		=3
	W		21

evil_woodworm: zad2: Jeżeli metoda akademicka to metoda wyznaczników, to: a) {2x + 3y +z = 8 {3x + y – 2z = 5 { x + 3y –z =−2 [ 8 3 1] W= [ 5 1 −2] =−2+9−6−1+12+9=21 [−2 3 −1] [ 8 3 1] W_x= [ 5 1 −2] =−8+15+12+2+15+48=84 [−2 3 −1] [2 8 1] W_y= [3 5 −2] =−10−6−16−5+24−8=−21 [1 −2 −1] [2 3 8] W_z= [3 1 5] =−4+72+15−8+18−30=63 [1 3 −2]

	Wx		84
x=		=		=4
	W		21

	Wy		−21
y=		=		=−1
	W		21

	Wz		63
z=		=		=3
	W		21

evil_woodworm: ugh... evil jak zwykle rozrabia−.− wczoraj wieczorem coś mi forum przestało działać. nie wiem czemu to się tyle razy wysłało_. sorry.

Bogdan: Do evil i kika22c. Niewłaściwe oznaczenia przy obliczaniu współrzędnych wektorów. Powinno być (pomijam nad nazwą wektora znak →): AB = [x_B − x_A, y_B − y_A], mają być w indeksach dolnych duże litery. Formuła zastosowana do wyznaczenia pola powierzchni trójkąta jest niewłaściwa (słyszałeś evil, że coś gdzieś dzwoni, ale nie wiesz, w którym kościele]] i przez to wynik jest błędny. Nie ma metody akademickiej rozwiązywania układu równań i nie można identyfikować tej nazwy z metodą wyznacznikową. Metodę wyznacznikową uczniowie poznają w szkole średniej, a niektórzy nauczyciele pokazują ten sposób rozwiązywania układów równań już w gimnazjum. Wartość wyznacznika W jest błędnie obliczona, nie sprawdzałem pozostałych wyznaczników. evil − do kitu z taką pomocą, należy Ci się za nią reprymenda.

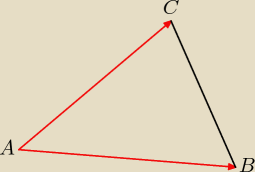
Bogdan: Zad. 3. A = (−2, −3), B = (2, 1), C = ( −1, 5). → AB = [4, 4] → AC = [1, 8] | 4 4 | P_Δ = ¹₂ | | | | = ¹₂ * |32 − 4| = 14 (wyznacznik II stopnia). | 1 8 |

evil_woodworm: przepraszam

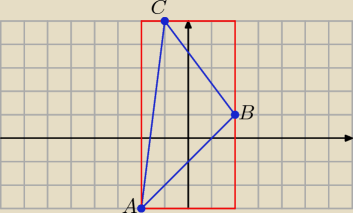
Bogdan: Ostatecznie można pole P_Δ trójkąta ABC wyznaczyć tak:

	1		1		1
PΔ = 4*8 − (		*4*4 +		*3*4 +		*1*8) = 32 − 18 = 14
	2		2		2

Myślę, że nie trzeba wyjaśniać szczegółów tego rachunku.

evil_woodworm: ech... wychodzi na to, że dla dobra ogółu powinno częściej mi to forum padać

Bogdan: No tak evil, mam nadzieję, że nie obraziłeś się na mnie. Przed wpisaniem tu jakiejś porady, rozwiązania, podpowiedzi, wskazówki, sprawdź przedtem wszystko dokładnie i oczywiście próbuj dalej, bo to jest skuteczna metoda na naukę tego przedmiotu

evil_woodworm: Bogdan, oczywiście, że się nie obraziłam. Nie obrażam się jeżeli ktoś mnie słusznie ochrzani −a tu mi się należało i tyle Ech, to jestem cała ja po prostu, wydaje mi się, że coś wiem/umiem, a później wychodzi jak zawsze Będę się starała poprawić

Bogdan: Przepraszam za zwracanie się do Ciebie evil jak do chłopca, będę teraz pamiętał, że jesteś dziewczyną. Pozdrawiam

evil_woodworm: Nic sie nie stalo

kika22c: a liczył ktoś może pozostałe zadania np 4, 5, 6 Bogdan może Ty pomożesz Dzięki wam za dotychczasową pomoc